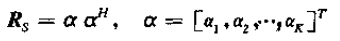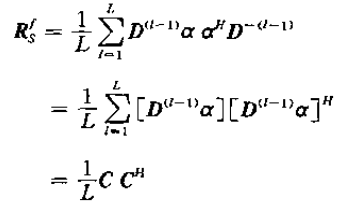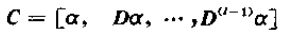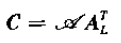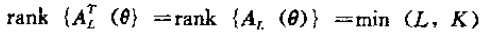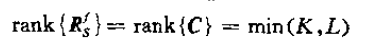作者：桂。
时间：2017-09-29 21:20:18
链接：http://www.cnblogs.com/xingshansi/p/7612984.html
前言
主要分析在解相干算法中，子阵平滑的有效性。
一、前向平滑
以均匀线阵（ULA）为例，第l个接收阵元的信号为：
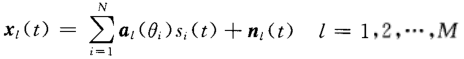
其中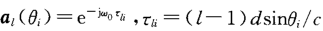
，M为阵元数，N为信号个数。
以前向平滑为例：
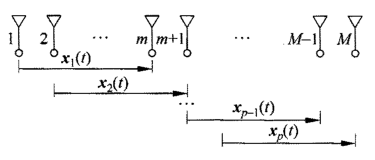
令β =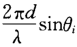 
，对于第k个子阵有
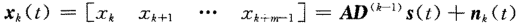
其中D为:
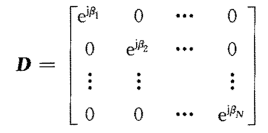
假设信号与噪声不相关，且噪声为白噪声，计算相关矩阵：
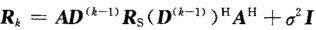
前向平滑修正的协方差矩阵：
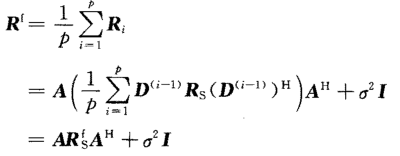
证明：当子阵阵元数m>=N，且当p>=N时，Rf为满秩矩阵。
对于相干情况，Rs的秩为1，故可以用矢量相乘的形式表示：
则
显然C与Rsf的秩是一致的。式中
C可进一步表示为
其中
，α为对应信号的幅度，因此该矩阵rank = K
AL是Vandermonde矩阵：
从而有：
进一步得出结论：
得证。
上面的推导是教科书中的推导，以两个子阵、两个信号为例，假设两个子阵的间距为D，对应的A可写为：
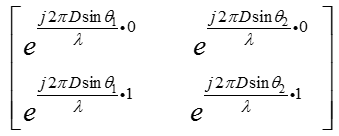
虽然具有Vandermonde结构，但即使入射角度不同，上面的矩阵仍然可能出现rank = 1的情况，只要满足（k为整数）：
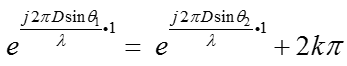
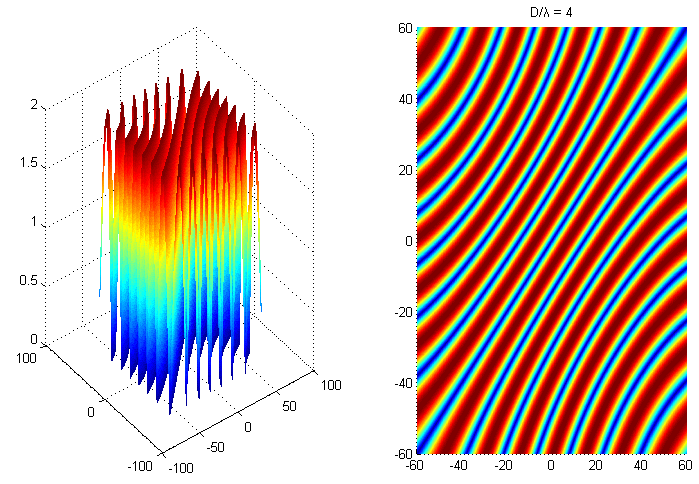
任意取D = 4*λ，theta1、2分别取-60°~60°，仿真结果：
D = 2*λ，进行仿真：
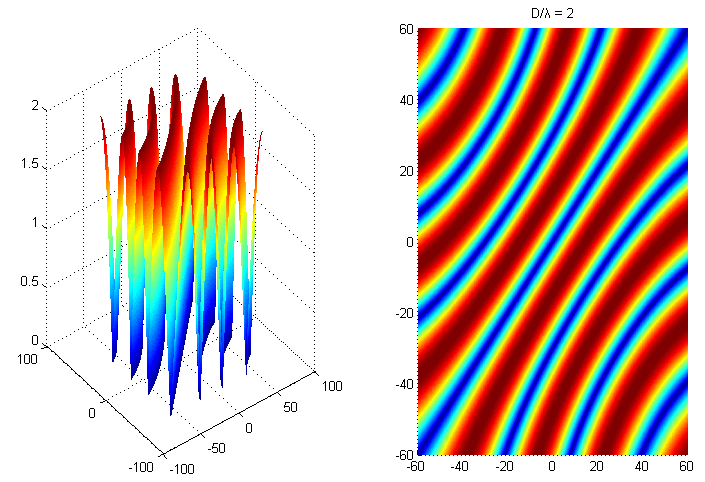
当两个相位差2pi整数倍，如图蓝线所示，此时相关矩阵的秩仍然是亏缺的，此时谱估计解相干失效，这里称蓝色区域为盲区。以MUSIC算法为例，自然也无从谈起矩阵分解以及谱估计。另一方面，D与λ比值的取值越小，则盲区越小。
这个盲区类似：子阵间距（孔径）减小，则相位模糊较少（盲区减少），但分辨率下降；子阵间距增大，则相位模糊增多（盲区增加），对应分辨率提高。
二、后向平滑算法
后向平滑：
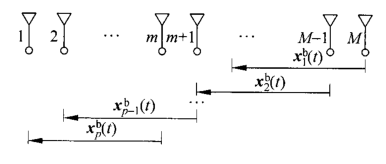
子阵信号为：
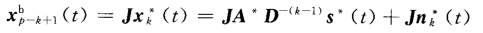
其中J为交换矩阵。
以第p-k+1个子阵为例：
后向空间平滑修正的相关矩阵为：
得出的性质与前向平滑类似。当子阵阵元数m>=N，且当p>=N时，Rb为满秩矩阵。
三、前后向平滑算法
前后向平滑，即是将前向平滑、后向平滑的相关矩阵累加。
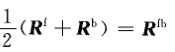
当子阵阵元数m>=N，且当2p>=N时，R为满秩矩阵。这一点仅当子阵结构为中心对称结构才成立。
四、前向、后向、前后向平滑与阵列的关系
前向平滑可以理解成原始子阵的平滑：
后向平滑则可以理解为镜像对称的虚拟（子阵）：
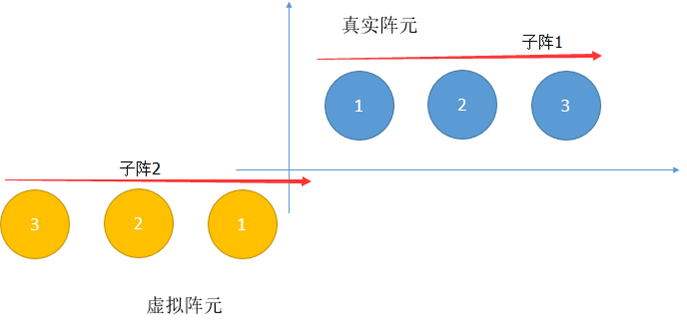
因为到原点的距离由d变为-d，在形式上体现的就是相位相反，也就是接收数据取共轭。顺序就是翻转，因此后向平滑就是前向平滑的共轭+翻转。
假设两个子阵的原始子阵为1、 2，翻转后为1‘，2’，前向平滑就是利用1，2；后向平滑为1‘，2’。前后向平滑为1，1‘，2，2’，由于形式上利用了更多的子阵，因此前后向平滑需要的子阵个数更少。但子阵必须中心对称，即镜像之后与原始子阵结构一致。
五、前后向与非均匀的关系
镜像的思路（即后向平滑），也给了非均匀布阵一些启发。
在构造子阵时，如果是一般的子阵，进行copy之后，即可利用空间平滑的思想：
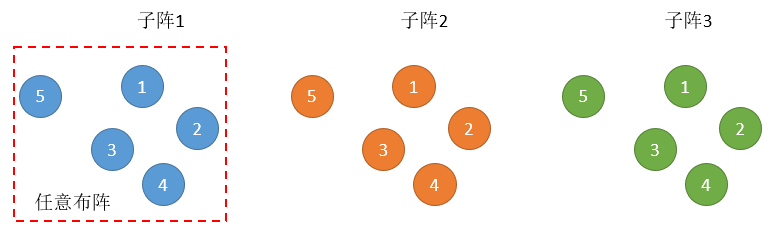
但可以借助镜像特性，进一步节省资源，例如一个5阵元的非均匀线阵：
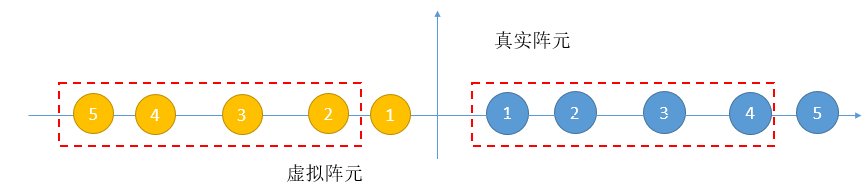
利用镜像的关系，可以得出两个4元的非均匀线阵（红框所示），这就给布阵拓展了思路。
六、非均匀镜像中坐标点的影响
该章节分析，从理论到结论，均错误。
根据上文第一部分的分析，子阵的间距D会造成盲区,且D/λ越大，盲区越大。
对于直接copy的空间平滑子阵思路，一旦子阵确定，子阵间距D也随之确定，因此盲区变得不可控。
而对于镜像的思路，子阵间距D是可控的，这就使得盲区变得相对可控。r对于上面提到的非均匀线阵，取不同的坐标原点：
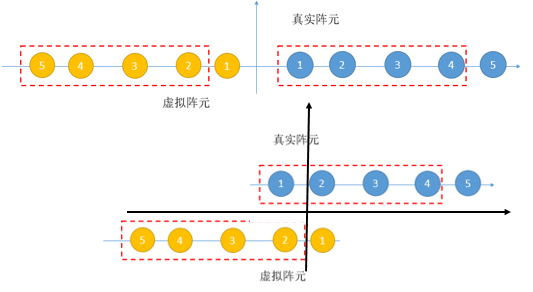
子阵之间的距离也随之改变，对于两个子阵，如果借助镜像的思想，理论上间距D可以取的范围是：0 - +∞。
这里就难免带来一个问题：改变坐标原点，即对应改变导向矢量，近而改变原始的阵列接收数据，可对于阵列来讲，接收的数据是固定不变的。这个可以换一个角度理解:X = AS，改变参考点，调节的是A，在X给定不变的情况下，S是一个相对的信息，尽管改变参考系可以使得盲区减小，但S可能得到的是小信号。一个解决办法是在谱估计（MUSIC为例）时取不同的参考系，假设X给定，从何借助两组数据进行DOA估计（镜像阵列，对于不同参考系，盲区不同。）