
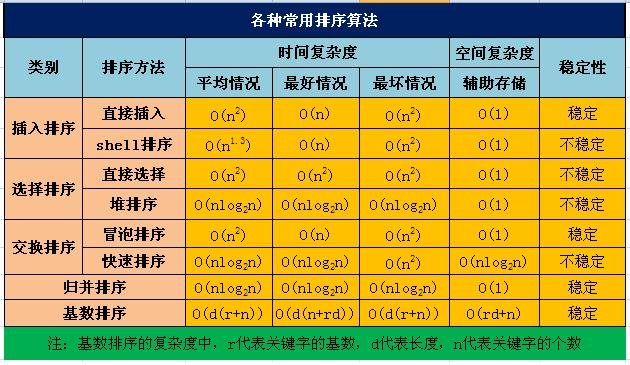
1、直接插入排序

直接插入排序的核心思想就是:将数组中的所有元素依次跟前面已经排好的元素相比较,如果选择的元素比已排序的元素小,则交换,直到全部元素都比较过。
因此,从上面的描述中我们可以发现,直接插入排序可以用两个循环完成:
第一层循环:遍历待比较的所有数组元素
第二层循环:将本轮选择的元素(selected)与已经排好序的元素(ordered)相比较。
如果:selected > ordered,那么将二者交换
2、希尔排序
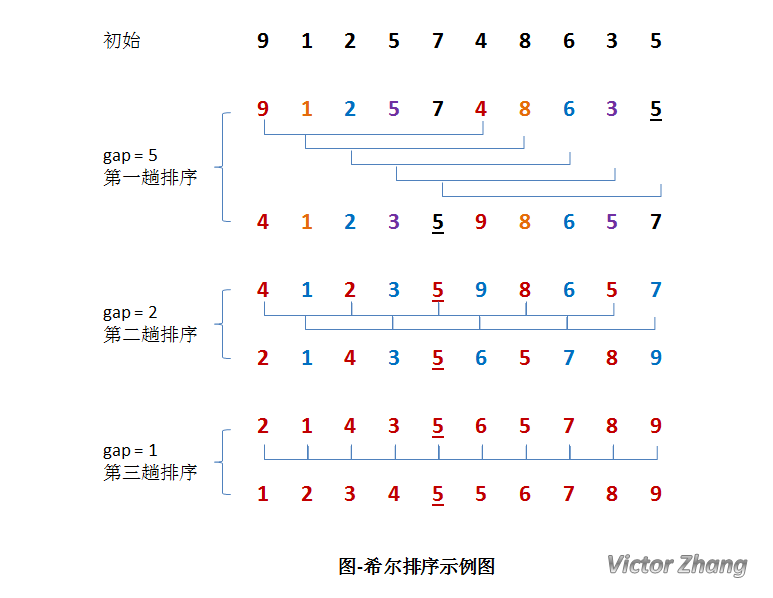
希尔排序的算法思想:将待排序数组按照步长gap进行分组,然后将每组的元素利用直接插入排序的方法进行排序;每次将gap折半减小,循环上述操作;当gap=1时,利用直接插入,完成排序。
同样的:从上面的描述中我们可以发现:希尔排序的总体实现应该由三个循环完成:
第一层循环:将gap依次折半,对序列进行分组,直到gap=1
第二、三层循环:也即直接插入排序所需要的两次循环。具体描述见上
3、简单选择排序
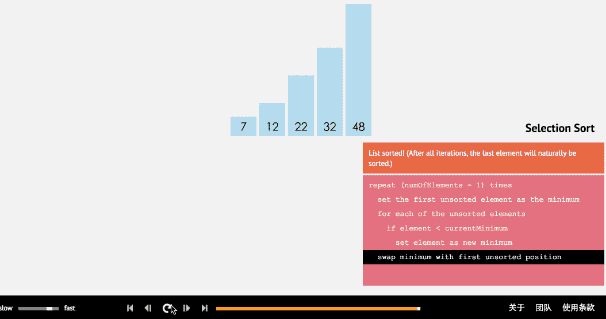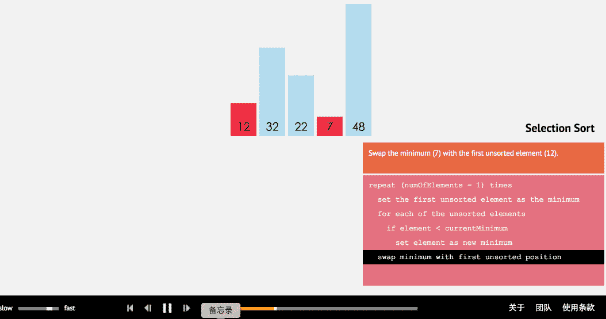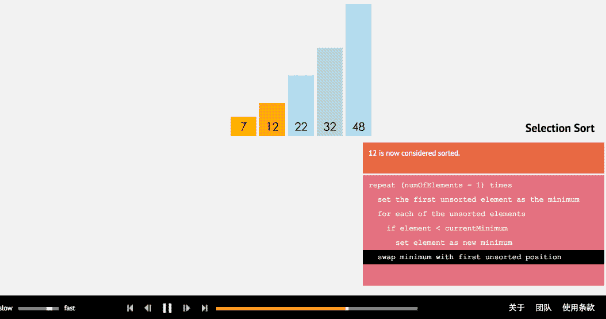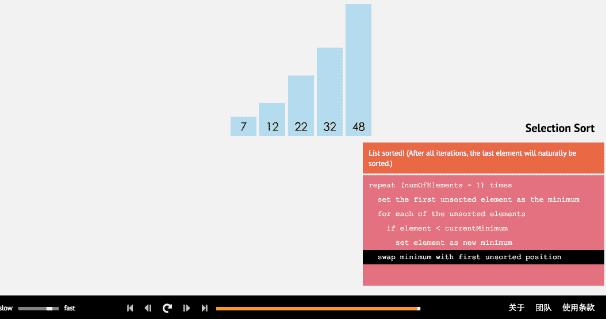
简单选择排序的基本思想:比较+交换。
- 从待排序序列中,找到关键字最小的元素;
- 如果最小元素不是待排序序列的第一个元素,将其和第一个元素互换;
- 从余下的 N - 1 个元素中,找出关键字最小的元素,重复(1)、(2)步,直到排序结束。
因此我们可以发现,简单选择排序也是通过两层循环实现。
第一层循环:依次遍历序列当中的每一个元素
第二层循环:将遍历得到的当前元素依次与余下的元素进行比较,符合最小元素的条件,则交换。
4、堆排序
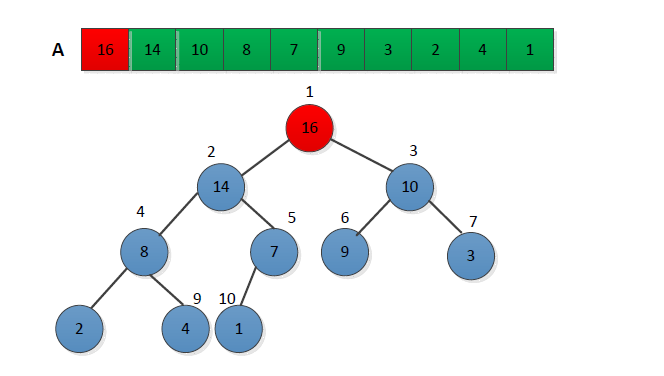
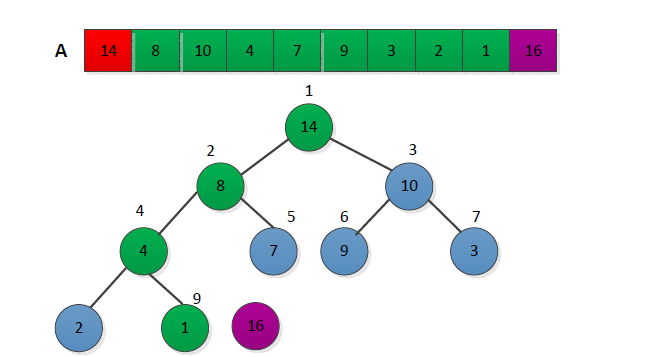
首先将序列构建称为大顶堆,将堆顶第一个元素放到最后,继续构建大顶堆,直至堆中只剩一个元素
5、冒泡排序(常见)

6、快速排序
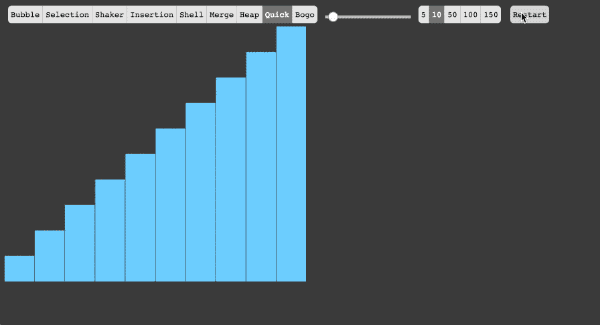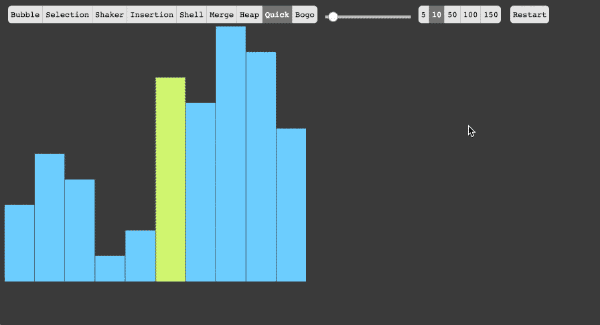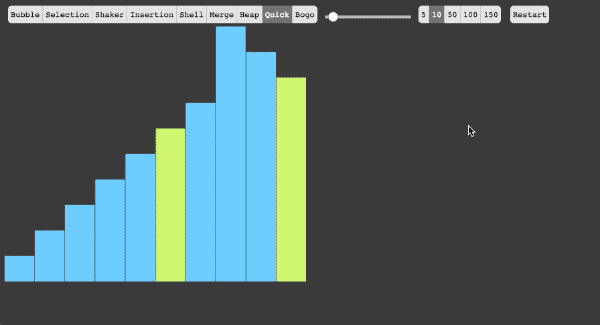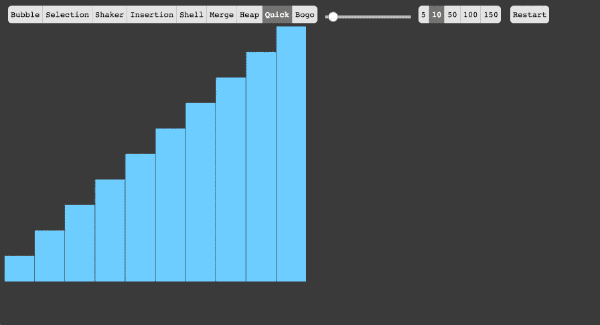
快速排序的基本思想:挖坑填数+分治法
- 从序列当中选择一个基准数(pivot)
在这里我们选择序列当中第一个数最为基准数 - 将序列当中的所有数依次遍历,比基准数大的位于其右侧,比基准数小的位于其左侧
- 重复步骤1.2,直到所有子集当中只有一个元素为止。
用伪代码描述如下:
1.i =L; j = R; 将基准数挖出形成第一个坑a[i]。
2.j--由后向前找比它小的数,找到后挖出此数填前一个坑a[i]中。
3.i++由前向后找比它大的数,找到后也挖出此数填到前一个坑a[j]中。
4.再重复执行2,3二步,直到i==j,将基准数填入a[i]中
7、归并排序

归并排序.gif
- 归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个典型的应用。它的基本操作是:将已有的子序列合并,达到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
- 归并排序其实要做两件事:
- 分解----将序列每次折半拆分
- 合并----将划分后的序列段两两排序合并
因此,归并排序实际上就是两个操作,拆分+合并
- 如何合并?
L[first...mid]为第一段,L[mid+1...last]为第二段,并且两端已经有序,现在我们要将两端合成达到L[first...last]并且也有序。
- 首先依次从第一段与第二段中取出元素比较,将较小的元素赋值给temp[]
- 重复执行上一步,当某一段赋值结束,则将另一段剩下的元素赋值给temp[]
- 此时将temp[]中的元素复制给L[],则得到的L[first...last]有序
- 如何分解?
在这里,我们采用递归的方法,首先将待排序列分成A,B两组;然后重复对A、B序列
分组;直到分组后组内只有一个元素,此时我们认为组内所有元素有序,则分组结束。
8、基数排序

- 基数排序:通过序列中各个元素的值,对排序的N个元素进行若干趟的“分配”与“收集”来实现排序。
分配:我们将L[i]中的元素取出,首先确定其个位上的数字,根据该数字分配到与之序号相同的桶中
收集:当序列中所有的元素都分配到对应的桶中,再按照顺序依次将桶中的元素收集形成新的一个待排序列L[ ]
对新形成的序列L[]重复执行分配和收集元素中的十位、百位...直到分配完该序列中的最高位,则排序结束 - 根据上述“基数排序”的展示,我们可以清楚的看到整个实现的过程