3.高斯滤波

一、高斯函数

1. 一维高斯函数

                                   

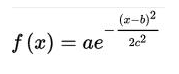
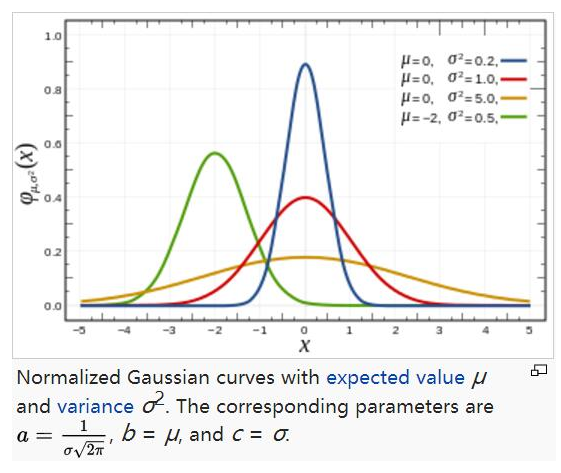
 对于任意的实数a,b,c，是以著名数学家Carl Friedrich Gauss的名字命名的。高斯的一维图是特征对称“bell curve”形状，a是曲线尖峰的高度，b是尖峰中心的坐标，c称为标准方差，表征的是bell钟状的宽度。

2. 二维高斯函数

       

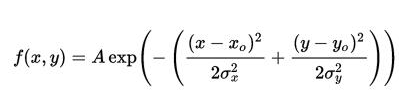
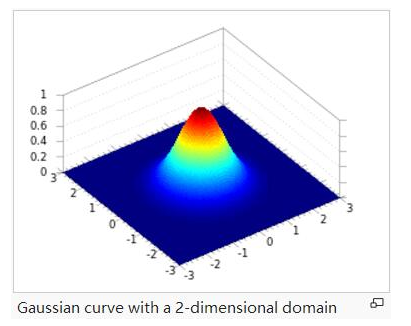
 A是幅值，x。y。是中心点坐标，σx σy是方差，图示如下，A = 1, xo = 0, yo = 0, σx = σy = 1

3.二维图像设计

说道“sigma表示的是标准差，如果标准差比较小，这是就相当于图像点运算，则平滑效果不明显；反之，标准差比较大，则相当于平均模板，比较模糊”，那么这么说可能很多人包括一开始的我并不是很理解，这是为什么呢，那么我们需要从高斯函数谈起：
                                               （期望为0时的特殊情况）

这样一个高斯函数的概率分布密度如下图所示：

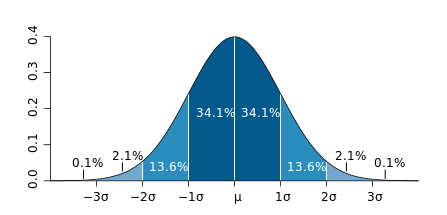
我们要理解好这个图，横轴表示可能得取值x，竖轴表示概率分布密度F(x)，那么不难理解这样一个曲线与x轴围成的图形面积为1。sigma（标准差）决定了这个图形的宽度，我给出下述结论：sigma越大，则图形越宽，尖峰越小，图形较为平缓；sigma越小，则图形越窄，越集中，中间部分也就越尖，图形变化比较剧烈。这其实很好理解，如果sigma也就是标准差越大，则表示该密度分布一定比较分散，由于面积为1，于是尖峰部分减小，宽度越宽（分布越分散）；同理，当sigma越小时，说明密度分布较为集中，于是尖峰越尖，宽度越窄！

理解好上述结论之后，那么（一）中的结论当然也就顺理成章了，sigma越大，分布越分散，各部分比重差别不大，于是生成的模板各元素值差别不大，类似于平均模板；sigma越小，分布越集中，中间部分所占比重远远高于其他部分，反映到高斯模板上就是中心元素值远远大于其他元素值，于是自然而然就相当于中间值得点运算。

二、高斯函数在图像设计中应用

    高斯噪声产生：图像常常受到一些随机误差的影响而退化，我们通常称这个退化为噪声。在图像的捕获、传输或者处理过程中都有可能产生、噪声，噪声可能是依赖于图像内容，可能无关。

            噪声一般由其频率的特征来刻画，理想的噪声称为白噪声，高斯噪声就属于白噪声的一种，为白噪声的一个特例。服从高斯（正态）分布。

   

   

namespace mycv {
    const double pi = 3.1415926;
    void createGaussianNoise(cv::Mat& src, cv::Mat& dst)
    {
        dst = src.clone();
        //1、灰阶范围[0， G - 1], 取sigma > 0; sigma越小噪声越小
        const int G = 256;
        double sigma = 20;
    
        for(int i = 0; i < src.rows; ++i)
            for (int j = 0; j < src.cols - 1; ++j)
            {
                //2、产生位于[0, 1]独立随机数gamma、phi
                std::random_device rd;
                std::mt19937 gen(rd());
                double gamma = std::generate_canonical<double, 2>(gen);
                double phi = std::generate_canonical<double, 2>(gen);
                //3、计算z1、z2
                double z1 = sigma * std::cos(2 * pi*phi)*std::sqrt(-2 * std::log(gamma));
                double z2 = sigma * std::sin(2 * pi*phi)*std::sqrt(-2 * std::log(gamma));
                //4、
                double tmpxy = src.at<uchar>(i, j) + z1;
                double tmpxy1 = src.at<uchar>(i, j + 1) + z2;

                //5
                if (tmpxy < 0)
                    dst.at<uchar>(i, j) = 0;
                else if (tmpxy > G - 1)
                    dst.at<uchar>(i, j) = G - 1;
                else
                    dst.at<uchar>(i, j) = static_cast<int>(tmpxy);

                
                if (tmpxy1 < 0)
                    dst.at<uchar>(i, j + 1) = 0;
                else if (tmpxy > G - 1)
                    dst.at<uchar>(i, j + 1) = G - 1;
                else
                    dst.at<uchar>(i, j + 1) = static_cast<int>(tmpxy1);

            }

    }
}//mycv

         实现高斯滤波：

        

// gaussian filter
cv::Mat gaussian_filter(cv::Mat img, double sigma) {
    int height = img.rows;
    int width = img.cols;
    int channel = img.channels();

    // prepare output
    cv::Mat out = cv::Mat::zeros(height, width, CV_8UC3);

    // prepare kernel
    int pad = floor(kernel_size / 2);
    int _x = 0, _y = 0;
    double kernel_sum = 0;

    // get gaussian kernel
    float kernel[kernel_size][kernel_size];

    for (int y = 0; y < kernel_size; y++) {
        for (int x = 0; x < kernel_size; x++) {
            _y = y - pad;
            _x = x - pad;
            kernel[y][x] = 1 / (2 * M_PI * sigma * sigma) * exp(-(_x * _x + _y * _y) / (2 * sigma * sigma));
            kernel_sum += kernel[y][x];
        }
    }

    for (int y = 0; y < kernel_size; y++) {
        for (int x = 0; x < kernel_size; x++) {
            kernel[y][x] /= kernel_sum;
        }
    }


    // filtering
    double v = 0;

    for (int y = 0; y < height; y++) {
        for (int x = 0; x < width; x++) {
            for (int c = 0; c < channel; c++)
            {

                v = 0;

                for (int dy = -pad; dy < pad + 1; dy++)
                {
                    for (int dx = -pad; dx < pad + 1; dx++)
                    {
                        if (((x - pad) > 0) && ((y - pad) > 0)&&((x + pad) < width) &&((y + pad) < height)) 
                        {
                            v += (double)img.at<cv::Vec3b>(y + dy, x + dx)[c] * kernel[dy + pad][dx + pad];
                        }
                    }
                }
                out.at<cv::Vec3b>(y, x)[c] = v;
            }
        }
    }
    return out;
}