之前一直在怀疑我是不是因为对CPN Tools的原理结构还是不够理解,对Petri网的还没有弄清楚,越往后面看这种质疑越来越严重。 之前说CPN Tools在对称和非对称算法中不能形式化的问题,后续看到的文献,虽然有对加解密做出示例,但是文献中并没有将如何加密和解密过程形式化,而是定义攻击者初始知识的解密函数,函数功能只能按照 case :k 其中k指代公钥,而函数输出是私钥。其实函数的功能相当于写了一对密钥对 (Pk,Sk),所以说并没有将 一个消息如何加密输出,和密文如何解密表达出来。这样 对协议中存在的对称和非对称加密算法就不能形式化。 内蒙古大学 [1] 关于CPN Tools协议分析这方面的的论文也没有真正定义如何实现对称和非对称算法。
1、ML 简单颜色集的定义
CPN ML 提供这些简单颜色集: Unit、 Boolean、Integer、String 、Enumerated、 Index (在CPN Tools中颜色集属性关键字是小写)
unit 颜色集包含单个元素:
colset name =unit [with new_unit] 如果没有token 名,与颜色集名字重合。在之前的博客中写过的灰姑娘例子中可以这样定义:
colset p=unit with pumpkin; colset c= unit with Cinderella; colset m=uint with mouse;
boolean颜色集定义: 其值为 true 或者 false :
colset name =bool [with (new_fale, new_true)] 选择的名字可以是 true 或者 false 。yes或者 no
colset Answer= bool with (no,yes);
Integers 颜色集定义: 是整形数字不是小数点。
colset name=int [with int-exp1... -exp3.... int.....int-expn] 将选择的数字限定在 定义的数字间隔之间。
colset Dozen= int with 1..12; 跟随整形变量的计算操作包括“ + - div mod abs Int.min Int.max ”
String 颜色集定义:定义字符串序列可由ASCII字符序列指定。用引号引起来。
colset name =string [with string-exp1........string-exp2] [and int-exp1....int-exp2] 指定字符的范围
colset LowerString =with "a"...."z"; 附加在String颜色集的操作运算包括 : -表示级联 , String.size ,substring
Enumerated 颜色集定义 :在声明中显示标识符
colset name =with id0 | id1 | ....idn;
colset g=with rice | wheat | oat;
Indexed 颜色集定义: 索引标识由索引标识符和说明值组成序列
colset PH =index ph with 1..5;
colset FR= index fork with 1..5;
2、ML复合颜色集的定义
复合颜色集是简单颜色集的组合。CPN 提供的复合颜色集有 : products ,records , unions, lists, subsets, aliases
其中 lists 和 unions两种 复合颜色集很少用到。
Products 和 records 两种颜色集都表示笛卡尔积的数据范围,不同之处在于 product 颜色集的组件没有名字,而record颜色集组件由自己的名字。
product 颜色集定义:
colset name = product name1*name2*.......namen;
(v1,v2......vn) 在 1<=i<=n之间 vi的类型为 namei ,提取第 i 个 product 声明的元素操作为:----> # i name
record 颜色集定义:
colset name = record id1:name1 * id2:name2 *........*idn:namen;
{id1=v1, id2=v2, ..... idn=vn} vi 是namei 类型的对应的值。 for 1<=i<=n .提取第 i record颜色集中的值操作: # idi name
在之前的博客中写过定义 EtherNet帧结构的颜色集定义, EtherNet帧结构构成: Source address 、 destination address 、 data 。我们定义MAC地址为integer颜色 ,帧数据为string 颜色集
colset MAC= int;
colset DATA=string;
colset frame =product MAC*MAC*DATA;
colset frame1= record src:MAC *dst:MAC *d:DATA
这里我们也就能看出 product 和 record复合颜色集之间的差异 。EtherNet帧使用了两种定义的方式,在实例化的时候也是不同的。如果是使用 frame 则值 X=(2,4,“Hello”) , 相同的值在frame1中的表达方式是 x1={src=2,dst=4, d="Hello"}
提取 frame颜色集中的目标地址操作: #2 x
提取frame1颜色集中的目标地址操作: # dst x1
alias 颜色集定义:别名颜色集合之前的的颜色集有相同的属性和值
colset name =name0
定义变量和常数:
变量是一个标识符,其值在模拟执行的时候可以改变,在Petri网中的元素铭文:
var id1 , id2 ..... idn:Cs_name ; 其中 idi 是标识符, Cs_name 是是之前定义的颜色集。我们可以这样定义 如下:
var f1,f2: frame;
var f3, f4:frame1;
将申明的值绑定到标识符上: 使用 val id=exp; 其中 id是标识符 exp 是 CPN ML表达式, 表示一个值绑定到一个表示符上,例如:
val CheckFrame= (3,5,“Ping”);
val ResponseFramel={src=5, dst=3, d="OK"} ;

函数的定义: CPN Tools中 只有逻辑函数,没有更进一步的复杂运算函数。 直到目前为止我查阅的文献中没有关于CPN Toll三可以形式化复杂函数,像 加解密哈数和 协议中出现的对称和非对称算法。

新限制变量是输出弧上的变量,没有绑定到输入弧和门卫上,当模型执行的时候分配一个随机值
函数 ran 生成衣蛾随机值,应用在大型颜色集中,

CPN Tools还提供特殊的随机数分布函数,像我们比较熟悉的伯努利分布函数,二项式分布函数,指数分布函数,爱尔朗分布函数,泊松分布函数等,那么这些特殊的函数这里不再讲了。

好现在我们就论文中出现的 如何将客户端和服务端之间选择密钥材料参数算法进行建模。
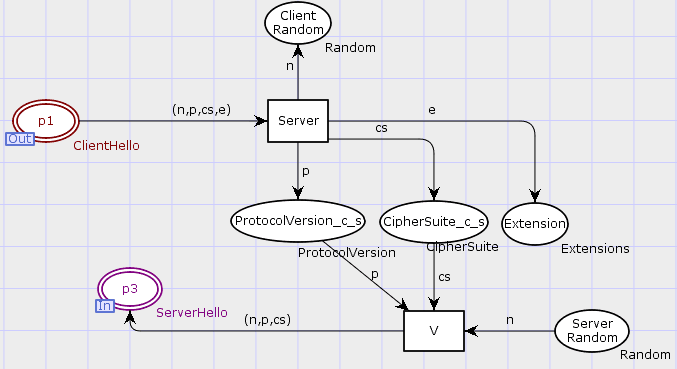
文献资料:
[1]白云莉. 基于CP-nets模型的安全协议形式化方法研究[D]. 2014.