线性代数之行列式(1) ——行列式的定义以及二阶行列式
使用消元法解二元线性方程组:

解决方式:
首先想办法干掉x2,那么第一个方程两边乘以a22,第二个方程两边乘以a12然后相减

同理可以得到x2的值:

若将方程组的系数按照原来的位置排成两行两列,则可以表示为以下的方式:

其中实线表示主对角线、虚线表示次对角线
可以看到得到的x1和x2的值得分母都是 ,即主对角线的元素的乘积减去次对角线的乘积。通常使用下面的记号表示:
,即主对角线的元素的乘积减去次对角线的乘积。通常使用下面的记号表示:
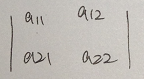
称为二阶行列式,其中aij(其中I,j=1,2)称为行列式第i行第j列的元素,行列式一般用字母D表示.二阶行列式表示的意义就是 .那么上面的方程组的解的分子可以表示为以下的行列式:
.那么上面的方程组的解的分子可以表示为以下的行列式:
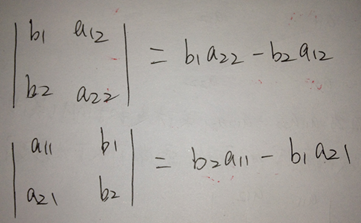
那么方程组的解可以表示为:

例子:使用行列式解以下线性方程组

解:
