1. 变换
在一个二维坐标系里,有一个向量 A = (2,1), (2,1) 这个数和向量图是一个变换。
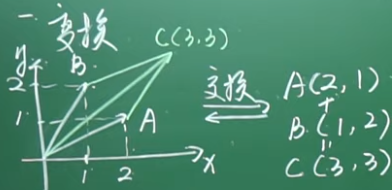
A(2,1) 表示 这个向量在X方向上有两个单位, Y方向上一个单位。
向量eX*向量eX = 向量eY*向量eY = 1
ex*ey=0, 那么ex和ey表示标准正交基、
2.傅里叶级数:周期性的函数 f(t) 可以变换成一系列正余玄函数的和
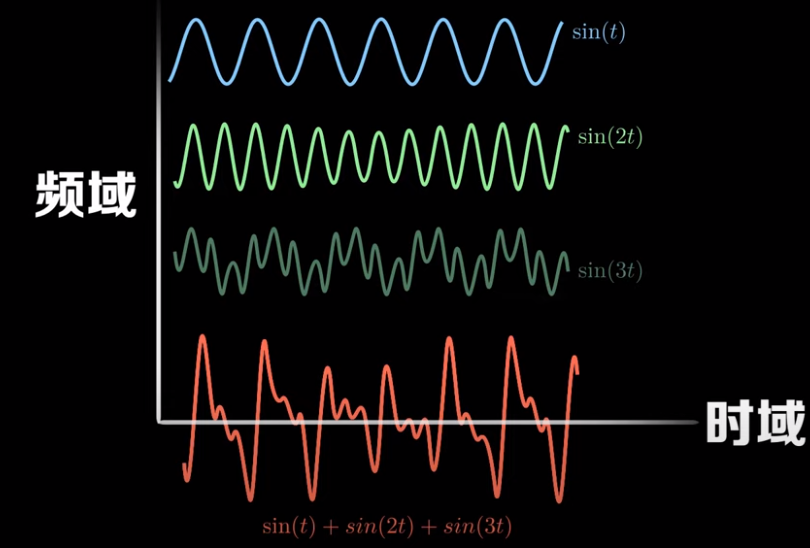
振幅和频率不同,频率为周期的长短,频率越大比如说3w,函数周期越小。
所以,任何一个波都可以分成不同的频率分量表示出来。
每一个频率的分量都有一个起始点,成为相位。
所以将一个时域的信号做了傅里叶变换后,会变成三个内容,第一,这个信号里包含的每个频率是啥;第二,每个频率下他的振幅是多少;第三, 每一个频率的相位是多少。
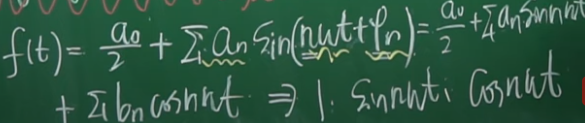
任何周期函数都可以用正交基(1, sin n*w*t, cos n*w*t)表示出来。
3.傅里叶变换或者连续傅里叶变换
将一个不是周期函数的信号看作是一个周期为无穷大的周期函数,让这个信号 f(t) 与一个正交基 e-jwt 做内积,如果内积完了信号为0,说明信号里面不含w的成分,因为只有sin wt 与sin wt 相乘才 或者 cos wt 与 cos wt 相乘才会出现1.
如果内积不等于0,则表示含w成分。 通过这样可以将一个不是周期的函数摘成很多不同的信号

4.应用
1. 声音的处理
给一个声音傅里叶变换后摘成不同的频率的信号,低频和高频。这样就可以给男生变女声,声音识别,以及可以提取一个人的声音的频率后模仿这个人的声音说任何话。
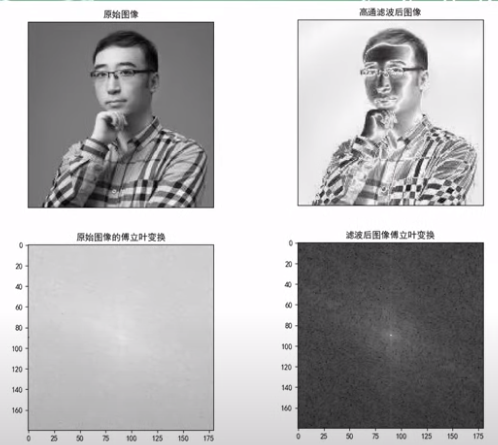
2. 图像
人的图像变换,磨皮等
将一个图像先进行傅里叶变换,里面有低频成分,如人的轮廓。高频成分,如细节,脸上的斑点等。
这时候过滤掉高频成分们就是过滤掉细节。