题意:求严格的次小生成树
严格次小生成树:(value(e)表示边e的权值) ∑e∈EM value(e)<∑e∈ES value(e)(EM为最小生成树边集,ES为次小生成树边集)
就是次小生成树边权和一定要小于最小生成树, 而非严格的就不一定,也可能等于。
非严格次小生成树求法:是在最小生成树边集外 找到一条边(假设两点为u,v)(一定大于等于最小生成树里的边),替换掉最小生成树中u,v之间最大边,使得两者差值最小。 主要是要保存最小生成树两点之间最大边。
严格次小生成树与非严格相似,但是要保存两点之间 最大边和次大边, 因为最小生成树边集外 的边等于最大边时,代替次大边否则就是代替最大边。 而这里用到了lca最近公共祖先,为了保证联通

如图:假设除去紫色的边是 最小生成树, 我们的目标是用紫色的边代替 环中的小于紫边最大的边。
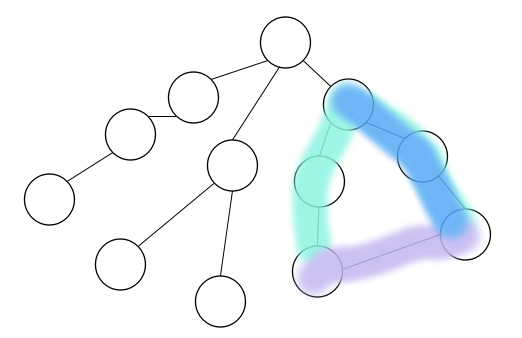
所以这里用到了lca,假设紫边两点为u,v, 先找到u,v的最近公共祖先点 fa,就分两边 找u,fa之间的最大小于紫边的边 和v,fa之间最大小于紫边的边
这样遍历每条不在最小生成树中的边,找到最小的 紫边与代替边的差值,加上最小生成树边权和就是答案。
最后我们来总结下步骤:
第一步:用kruskal 找到最小生成树,记算边权和,和 标记最小生成树中的边。
第二步:dfs搜索 记录最小生成树中两点的最近公共祖先, 并用同样的方式记录 两点之间最大边和最次边。
第三步:枚举不在最小生成树中的边,lca找到边两点的最近公共祖先,分两边查找最大小于这条边的边权值。
最后:找到最小的差值加上最小生成树边权和即可。
代码中一直贯彻着倍增的思想。详细可以看代码:
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define inf 0x3f3f3f3f using namespace std; typedef long long ll; const int maxn=1e5+100; const int maxm=3e5+100; struct node{ int u,v,w,nxt; }e[2*maxm]; struct edge{ int x,y,z,tag; }ee[maxm]; int head[maxn],bz[maxn][22];//bz[i][j]记录i的2^j祖先 int maxi[maxn][22],mini[maxn][22],lg[maxn]; //maxi[i][j],记录i到2^j祖先之间的最大边权值,mini是记录次边值 //lg[i]表示log_2(i)+1,用来优化lca的,可以不用 int depth[maxn],fa[maxn],n,m,cnt; bool cmp(edge a,edge b) { return a.z<b.z; } void add(int u,int v,int w) { e[cnt].u=u; e[cnt].v=v; e[cnt].w=w; e[cnt].nxt=head[u]; head[u]=cnt++; } void dfs(int f,int fath)//记录最小生成树中两点之间的最近公共祖先和最大边,次大边 { bz[f][0]=fath; depth[f]=depth[fath]+1; for(int i=1;(1<<i)<=depth[f];i++) { bz[f][i]=bz[bz[f][i-1]][i-1];//lca中的核心转换 mini[f][i]=max(mini[f][i-1],mini[bz[f][i-1]][i-1]); maxi[f][i]=max(maxi[f][i-1],maxi[bz[f][i-1]][i-1]); if(maxi[f][i-1]!=maxi[bz[f][i-1]][i-1]) mini[f][i]=max(mini[f][i],min(maxi[f][i-1],maxi[bz[f][i-1]][i-1])); } for(int i=head[f];i!=-1;i=e[i].nxt) { if(e[i].v!=fath) { maxi[e[i].v][0]=e[i].w; mini[e[i].v][0]=-1; dfs(e[i].v,f); } } } int lca(int x,int y)//lca求最近公共祖先 { if(depth[x]<depth[y])//使x深度大于y swap(x,y); while(depth[x]>depth[y])//跳到相同深度 x=bz[x][lg[depth[x]-depth[y]]-1]; if(x==y) return x; for(int k=lg[depth[x]]-1;k>=0;k--)//往上找,直到x,y跳到最近公共祖先的下一节点 if(bz[x][k]!=bz[y][k]) x=bz[x][k],y=bz[y][k]; return bz[x][0];//返回最近公共祖先 } int find(int x) { return fa[x]==x?x:fa[x]=find(fa[x]); } int qmax(int u,int v,int w)//找到u,v之间小于 w大最大边 { int ans=-inf; for(int i=lg[depth[u]]-1;i>=0;i--) { if(depth[bz[u][i]]>=depth[v]) { if(w!=maxi[u][i])//不等于最大边,取最大边 ans=max(ans,maxi[u][i]); else//等于,取次大边 ans=max(ans,mini[u][i]); u=bz[u][i];//往上跳 } } return ans; } int main() { cnt=0; ll sum=0; memset(head,-1,sizeof(head)); scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) fa[i]=i; for(int i=1;i<=n;i++)//lca常数优化,lg[i]表示log_2(i)+1; lg[i]=lg[i-1]+(1<<lg[i-1]==i); for(int i=1;i<=m;i++) scanf("%d%d%d",&ee[i].x,&ee[i].y,&ee[i].z); sort(ee+1,ee+m+1,cmp); for(int i=1;i<=m;i++)//kruskal { int fx=find(ee[i].x); int fy=find(ee[i].y); if(fx!=fy) { sum+=ee[i].z; ee[i].tag=1; fa[fx]=fy; add(ee[i].x,ee[i].y,ee[i].z); add(ee[i].y,ee[i].x,ee[i].z); } } dfs(1,0); int ans=inf; for(int i=1;i<=m;i++)//枚举不在最小生成树的边 { if(!ee[i].tag) { int lc=lca(ee[i].x,ee[i].y); int res=max(qmax(ee[i].x,lc,ee[i].z),qmax(ee[i].y,lc,ee[i].z)); ans=min(ans,ee[i].z-res);//ans寻找最小差值 } } printf("%lld ",sum+ans);//答案就是最小生成树边权和加最小差值 return 0; }