正态分布

用来计算连续变量的发生率，说的很抽象，简单说就是单独拿出来没什么太大用，但并不是说这个没什么用，相反这个太重要了，这玩意能让你看清世界的真相

先看个图，像这样的线性就是正太分布

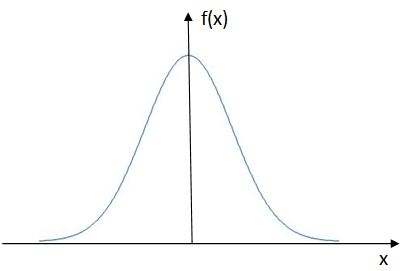这是一个标准的正态分布

正太分布有4个特点

      呈钟形分布，是对称的

      分布的集中趋势(均值、中位数、众数)都一样

      中间最高的部分等于1.3倍的标准差

      随机变量分布区间无限制

模型函数f(X) = (1/2πσ^0.5)*e^(-(1/2)*(((X-μ)/σ)^2))，e是自然常数，已经说过了这次略过，μ是总体均值，可以用函数算出，σ是总体标准差，也可以用函数算出，X则是随机变量

一个标准正太分布函数的μ = 0，σ = 1，这个看起来有点扯的事其实还是存在的

标准正态分布函数f(Z) = (1/2π)*e^(-1/2*Z^2)

这次牛逼了，一次写两个函数，来了

# 正态分布函数
def normal_fun(chance_x, case_list = [0], mean_num = 0, covar_num = 0):
  e = 2.7182818
  pal = 3.1415926
  if len_fun(case_list) == 1 and case_list[0] == 0:
    normal_num = (1 / (covar_num * ((2 * pal) ** 0.5))) * e ** ((0-0.5)*(((chance_x-mean_num)/covar_num) ** 2))
  else:
    mean_num = sum_mean_fun(case_list)
    covar_num = covar_fun(case_list)
    normal_num = (1 / (covar_num * ((2 * pal) ** 0.5))) * e ** ((0-0.5)*(((chance_x-mean_num)/covar_num) ** 2))
  return normal_num

函数说明：实际需要3个参数，随机变量、期望值、协方差，因此函数有两种用法

if __name__ == '__main__':
  # 第一种用法
  case_list = [8,9,10,11,12]
  normal_rate = normal_fun(3,case_list = case_list)
  print normal_rate
  # 第二种用法
  normal_rate = normal_fun(3,mean_num = 0,covar_num = 1)
  print normal_rate

第二种就是图中的标准正态分布函数，要求μ = 0，σ = 1，因此省略这两个传参

# 标准正太分布函数
def normal_s_fun(chance_x):
  e = 2.7182818
  pal = 3.1415926
  normal_num = (1 / ((2 * pal) ** 0.5)) * e ** ((0-0.5) * (chance_x ** 2))
  print normal_num

本来想多写点什么的，可是感觉什么和这个都不搭，就把这个单独拎出来放这了