Ex 6_12 凸多边形的最优三角剖分..._第六次作业

假设顶点的总数为n，从0到n-1. 从序号为0的顶点开始以逆时针方向排序，对于

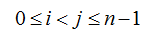
令子问题A[i,j]为包含顶点i,i+1, . . . j的凸多边形的最小三角剖分代价，dist(i,j)为顶点i到顶点j的距离。对于子问题A[i,j],考虑边e(i,j)最终会在某个三角形内，为了找出这个三角形，计算i到j之间的每个顶点k与i和j围成的三角形的对角线的和的最小值即为A[i,j]，找出对角线和的最小值所对应的k,再继续查找A[i,k],A[k,j],直到多边形不能再划分为止，因此的到递推式

package org.xiu68.ch06.ex6;

public class Ex6_12 {

    public static Point[] ps1,ps2;
    //凸多边形的最优三角形剖分，求所有对角线之和的最小值
    public static void main(String[] args) {
        // TODO Auto-generated method stub        
        /*
         最小三角剖分代价为：8.47213595499958
        三角形划分方式为：
        Point:0,Point:4,Point:1
        Point:1,Point:4,Point:2
        */
        ps1=new Point[]{
                new Point(2,0),
                new Point(0,2),
                new Point(0,4),
                new Point(4,4),
                new Point(4,2)
        };
        int[][] arr1=new int[ps1.length][ps1.length];
        minTriangle(ps1,arr1);   //8.47213595499958
        System.out.println("三角形划分方式为：");
        divide(arr1,0,ps1.length-1);
        
        /*
         最小三角剖分代价为：11.21110255092798
        三角形划分方式为：
        Point:0,Point:5,Point:1
        Point:1,Point:5,Point:3
        */
        System.out.println();
        ps2=new Point[]{
                new Point(0,2),
                new Point(10,4),
                new Point(12,4),
                new Point(13,2),
                new Point(12,0),
                new Point(10,0)
        };
        int[][] arr2=new int[ps2.length][ps2.length];
        minTriangle(ps2,arr2);  //11.21110255092798
        System.out.println("三角形划分方式为：");
        divide(arr2,0,ps2.length-1);
    }
    
    //B中存放三角形的第三个顶点
    public static void minTriangle(Point[] ps,int[][] B){
        double[][] A=new double[ps.length][ps.length];        //子问题A[i][j]的最优三角剖分代价
        
        for(int i=0;i<A.length;i++)
            for(int j=0;j<A[i].length;j++){
                A[i][j]=0;
                B[i][j]=0;
            }
        
        for(int s=4;s<=ps.length;s++){                      //包含s个顶点的多边形的最优剖分代价    
            for(int i=0;i<ps.length-s+1;i++){                //包含s个顶点的多边形的开始顶点，以逆时针方向前进
                int j=i+s-1;                                //包含s个顶点的多边形的结束顶点
                A[i][j]=Double.MAX_VALUE;
                double temp=A[i][j];

                                                        //t为i和j的相对顶点，从i的后一个顶点开始，结束顶点为j的前一个顶点
                for(int t=i+1;t<=j-1;t++){
                    if(t==i+1){                         //t为i的后一个顶点
                        temp=dist(ps,t,j)+A[t][j];
                    }
                    else if(t==j-1){                       //t为j的前一个顶点
                        temp=dist(ps,i,t)+A[i][t];
                    }else{                               //t处于i的后一个顶点之后，j的前一个顶点之前
                        temp=dist(ps,i,t)+dist(ps,j,t)+A[i][t]+A[t][j];
                    }
                    if(A[i][j]>temp){
                        A[i][j]=temp;
                        B[i][j]=t;
                    }
                }//3
            }//2
        }//1
        System.out.println("最小三角剖分代价为："+A[0][ps.length-1]);
    }
    
    public static void divide(int[][] B,int i,int j){
        if(B[i][j]!=0){
            System.out.println("Point:"+i+",Point:"+j+",Point:"+B[i][j]);
            divide(B,i,B[i][j]);
            divide(B,B[i][j],j);
        }
    }
    
    //顶点序号i和j之间的距离
    public static double dist(Point[] ps, int i,int j){
        double m1=Math.pow(ps[i].x-ps[j].x, 2);
        double m2=Math.pow(ps[i].y-ps[j].y, 2);
        return Math.sqrt(m1+m2);
    }
    
}

class Point{
    public double x;
    public double y;
    public Point(double x,double y){
        this.x=x;
        this.y=y;
    }
}