1.什么是非负矩阵分解?
NMF的基本思想可以简单描述为:对于任意给定的一个非负矩阵V,NMF算法能够寻找到一个非负矩阵W和一个非负矩阵H,使得满足 ,从而将一个非负的矩阵分解为左右两个非负矩阵的乘积。如下图所示,其中要求分解后的矩阵H和W都必须是非负矩阵。
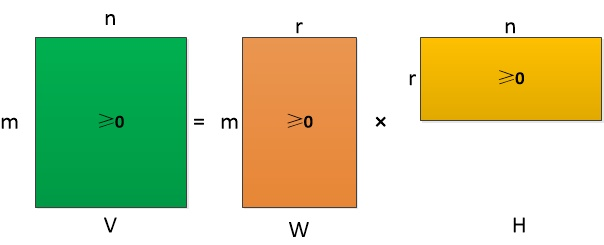
分解前后可理解为:原始矩阵 的列向量是对左矩阵
的列向量是对左矩阵 中所有列向量的加权和,而权重系数就是右矩阵对应列向量的元素,故称
中所有列向量的加权和,而权重系数就是右矩阵对应列向量的元素,故称 为基矩阵,
为基矩阵, 为系数矩阵。一般情况下
为系数矩阵。一般情况下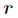 的选择要比
的选择要比 小,即满足
小,即满足 ,这时用系数矩阵代替原始矩阵,就可以实现对原始矩阵进行降维,得到数据特征的降维矩阵,从而减少存储空间,减少计算机资源。
,这时用系数矩阵代替原始矩阵,就可以实现对原始矩阵进行降维,得到数据特征的降维矩阵,从而减少存储空间,减少计算机资源。
2.非负矩阵分解一个示例解释

通过图1中的面部特征提取例子可领略NMF处理数据的方式。最左边的大矩阵由一系列的小图组成,这些小图是分析数据库中包含的2429个脸部图像的结果,每幅图像由19×19个像素组成。传统方法中这样的小图是一幅完整的人脸图像,但是在NMF方法中,每个小图是通过一组基图像乘以一个权重矩阵而产生的面部特征图,经过这样处理的每幅小图像恰好表示了诸如“鼻子”、“嘴巴”、“眼睛”等人脸局部概念特征,这便大大压缩了存放的图像数据量。左边的大矩阵由每幅小图像的19列一起组成矩阵的一列,那样它就是19×19=361行,2429列。这个例子中,NMF方法用基图像来代表眼、眉毛、鼻子、嘴、耳朵、胡子等,它们一起组成了数据库中的脸。这样给人最先的直觉就是它很好地压缩了数据。事实上Lee和Seung在他们的论文中更深入地指出,与人类识别事物的过程相似,NMF也是一种优化的机制,近似于我们的脑分析和存储人脸数据的过程。这个例子中,原图像表示这些局部特征的加权组合,这与人类思维中“局部构成整体”的概念是相吻合的。因此,NMF算法似乎体现了一种智能行为。
3.非负矩阵分解NMF的应用
(1)图像分析 NMF最成功的一类应用是在图像的分析和处理领域
(2)文本聚类,数据挖掘
(3)语音处理
(4)机器人控制
(5)生物医药工程和化学工程