1.什么是K-Means?
K均值算法聚类
关键词:K个种子,均值
聚类的概念:一种无监督的学习,事先不知道类别,自动将相似的对象归到同一个簇中
K-Means算法是一种聚类分析(cluster analysis)的算法,其主要是来计算数据聚集的算法,主要通过不断地取离种子点最近均值的算法.
K-Means算法的思想很简单,对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大.
2.k-Means原理
每次计算距离采用的是欧式距离
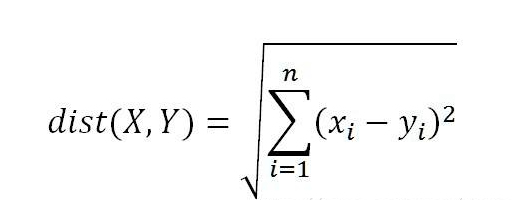
步骤图:
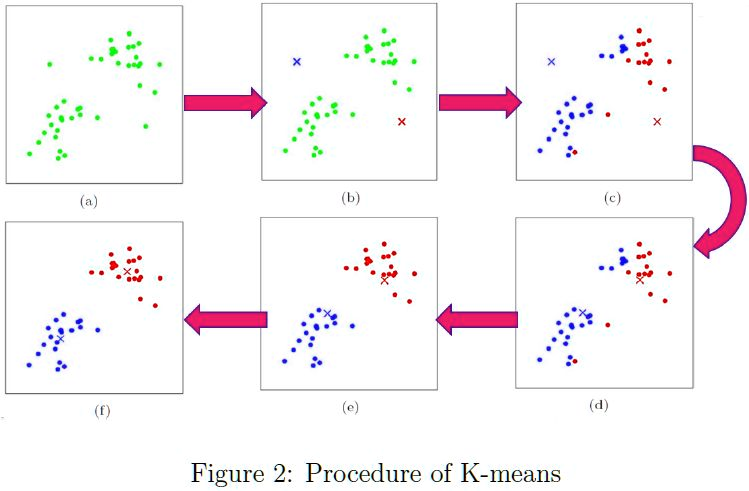
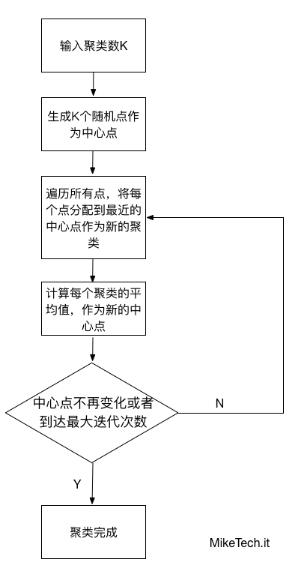
步骤总结:
- 从数据中选择k个对象作为初始聚类中心;
- 计算每个聚类对象到聚类中心的距离来划分;
- 再次计算每个聚类中心
- 2~3步for循环,直到达到最大迭代次数,则停止,否则,继续操作。
- 确定最优的聚类中心
主要优点:
- 原理比较简单,实现也是很容易,收敛速度快。
- 聚类效果较优。
- 算法的可解释度比较强。
- 主要需要调参的参数仅仅是簇数k。
- 当簇近似为高斯分布时,效果是最高的.
- 对处理大数据集该算法保持可伸缩性和高效率
主要缺点:
-
K-Means算法需要用初始随机种子点来搞,这个随机种子点太重要,不同的随机种子点会有得到完全不同的结果。(K-Means++算法可以用来解决这个问题,其可以有效地选择初始点)
- 必须事先给出k(要生成的簇的数目),而且对初值敏感,对于不同的初值,可能会导致不同的结果.
- 对于不是凸的数据集比较难收敛
- 如果各隐含类别的数据不平衡,比如各隐含类别的数据量严重失衡,或者各隐含类别的方差不同,则聚类效果不佳。
- 采用迭代方法,得到的结果只是局部最优。
- 对噪音和异常点比较的敏感。
3.K-Means算法应用:
- 对于多维数据的分类,效果很好
- 二维坐标点的X,Y 坐标,其实是一种向量,是一种数学抽象。现实世界中很多属性是可以抽象成向量的,比如,我们的年龄,我们的喜好,我们的商品,等等,能抽象成向量的目的就是可以让计算机知道某两个属性间的距离。如:我们认为,18岁的人离24岁的人的距离要比离12岁的距离要近,鞋子这个商品离衣服这个商品的距离要比电脑要近,等等。解决实际问题比较好
4.K-Means实例-亚洲国家队足球水平分类
1 import numpy as np 2 3 import pandas as pd 4 5 # cluster :簇,一堆 6 # 只有分类 7 from sklearn.cluster import KMeans 8 9 import matplotlib.pyplot as plt 10 %matplotlib inline 11 12 from mpl_toolkits.mplot3d.axes3d import Axes3D 13 import warnings 14 warnings.filterwarnings('ignore') 15 16 # 2006年世界杯,2010年世界杯,2007亚洲杯,比赛数据 17 football = pd.read_csv('./AsiaFootball.txt') 18 19 X = football.iloc[:,1:] 20 21 kmeans = KMeans(n_clusters=5) 22 23 # 无监督学习 PCA也是无监督 NMF无监督 24 kmeans.fit(X) 25 y_ = kmeans.predict(X) 26 27 # 分成3类 28 for i in range(3): 29 index = np.argwhere(y_ == i).reshape(-1) 30 print('类别是%d国家队有:'%(i),football['国家'].loc[index].get_values()) 31 32 # 分成5类 33 for i in range(5): 34 index = np.argwhere(y_ == i).reshape(-1) 35 print('类别是%d国家队有:'%(i),football['国家'].loc[index].get_values())
加载的数据结构:
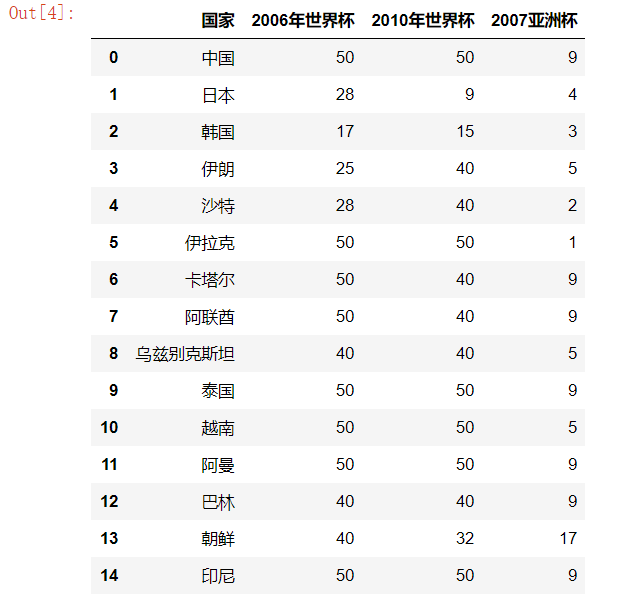
分成3类打印输出:

分成5类打印输出:

分类好了,但是我们不知道分成4类好还是分成5类好,现在选取一些指标来评判一下:
(1)轮廓系数 Silhouette Coefficient
1 # 轮廓系数 2 from sklearn.metrics import silhouette_score 3 4 for i in range(2,16): 5 kmeans = KMeans(n_clusters=i) 6 kmeans.fit(X) 7 y_ = kmeans.predict(X) 8 s = silhouette_score(X,y_) 9 print('聚类个数是:%d。轮廓系数是:%0.2f'%(i,s))
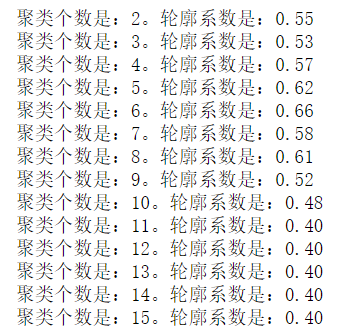
由轮廓系数分析可知,当分为6类的时候,效果最好
(2)calinski_harabasz_score CH分数(值越大,效果越好)
1 for i in range(2,16): 2 kmeans = KMeans(n_clusters=i) 3 kmeans.fit(X) 4 y_ = kmeans.predict(X) 5 s = metrics.calinski_harabasz_score(X,y_) 6 print('聚类个数是:%d。calinski_harabasz_score:%0.2f'%(i,s))
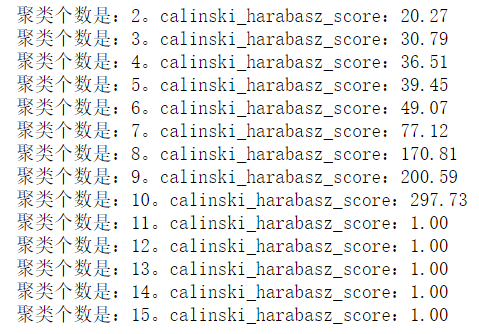
(3)davies_bouldin_score 戴维森堡丁指数DBI(度量是每个聚类最大相似度的均值)
1 for i in range(2,16): 2 kmeans = KMeans(n_clusters=i) 3 kmeans.fit(X) 4 y_ = kmeans.predict(X) 5 s = metrics.davies_bouldin_score(X,y_) 6 print('聚类个数是:%d。davies_bouldin_score:%0.2f'%(i,s))
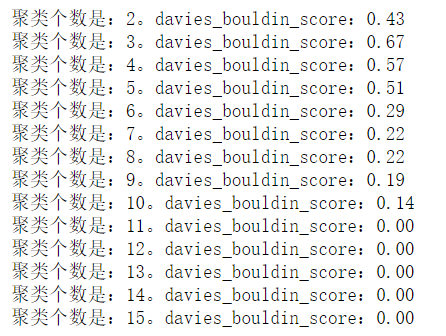
以上三种方式得到的最优分类均不同,这是因为数据的原因,数据不太好.
5.Kmeans评价指标,这个就是聚类的衡量指标,之后再具体详细的解释一下
(1)轮廓系数 metrics.silhouette_score
(2)兰德系数 metrics.adjusted_rand_score
(3)互信息指标 metrics.adjusted_mutual_info_score
(4)同质性 homogeneity_completeness_v_measure
(5)Calinski-Harabasz索引 metrics.calinski_harabasz_score
(6)Davies-Bouldin索引 metrics.davies_bouldin_score
补充:
1.k-Means算法,初值的选择,对聚类结果有影响吗?
k-Means是初值敏感的,举个例子:
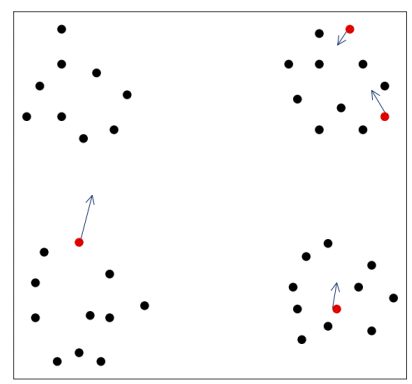
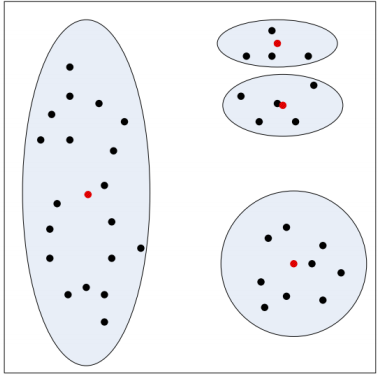
对于左图来说,使用k-means分类,我们肉眼可见,选择初值会在四个区域选择四个样本,
但是如图所示,在第二部分选择了两个样本作为初始值,而第一部分没有选择,
这种情况下,最终的分类结果可能是右图所示,这样的话结果就不太好,分类效果明显不好,
所以,由此可见,初值的选择对分类有很大的影响.
我觉得有一种解决方法是:
k-means++算法:
先随机选择一个样本点为初始值,然后计算其他所有样本到该该本点的距离,然后计算加权平均,相当于给每个样本点一个权值,也就是被选中的概率,然后按照概率选择其他的初始值,并不是概率高的一定会被选中,概率低的也可能会被选中,这是一个概率问题,一般来说选中都是距离第一个初始值比较远的,这样我们就有下一个聚类中心了,再然后找第三个聚类中心的话,更新一下之前的距离权值,根据样本到两个聚类中心的距离,哪个距离大选择哪个,这样再根据概率挑选出第三个聚类中心,之后的步骤是一样的,这就是k-means++算法
2.k-means使用场景
k-means其实对样本的分布是有要求的,我们认为k个样本其实是服从高斯混合分布的,并且每个高斯分布的方差是一样的,其实也就是每个簇的方差是一样的.
3.k-means的公式化解释:
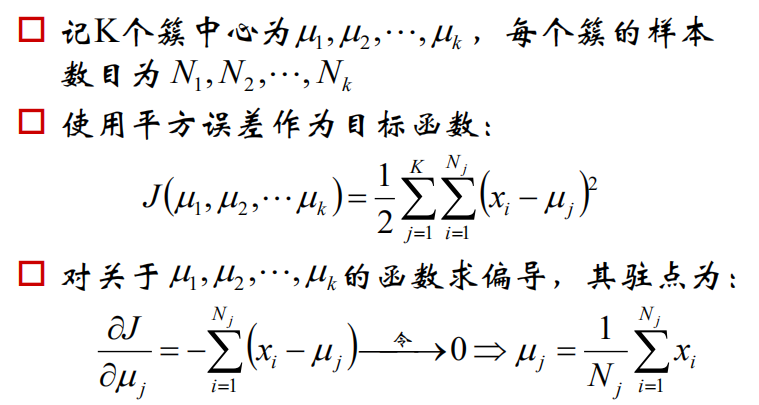
我们上边所说的原理其实就是两个公式的重复循环
4.如果样本量巨大的话,可以考虑使用mini-batch k-means算法
5.k-means算法可能会振荡
采用迭代的方法,多做几次,每次结果可能都不一样,具体哪个效果好,可能需要人为去判断.