一、希尔排序(Shell Sort)
希尔排序(Shell Sort)是一种分组插入排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序,同时该算法是冲破O(n2)的第一批算法之一。
1、算法思路
首先取一个整数d1=n/2,将元素分为d1个组,每组相邻量元素之间距离为d1,在各组内进行直接插入排序;
取第二个整数d2=d1/2,重复上述分组排序过程,直到di=1,即所有元素在同一组
希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序;最后一趟排序使得所有数据有序。
2、算法思路图解
例如有一个列表有九个元素如下所示:

(1)第一趟排序
取d1=9/2得到d1=4,将整个列表分为4组,每组相邻元素间距离为4:
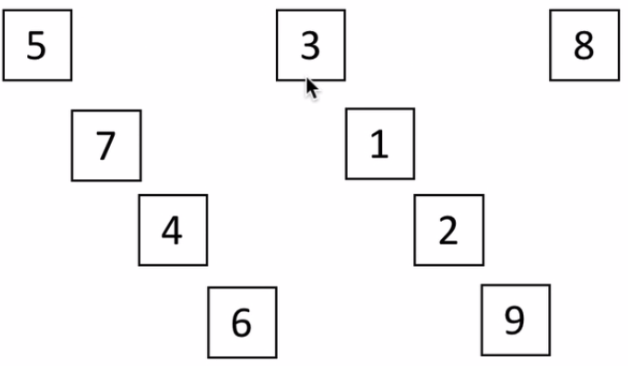
将各个组内进行插入排序:
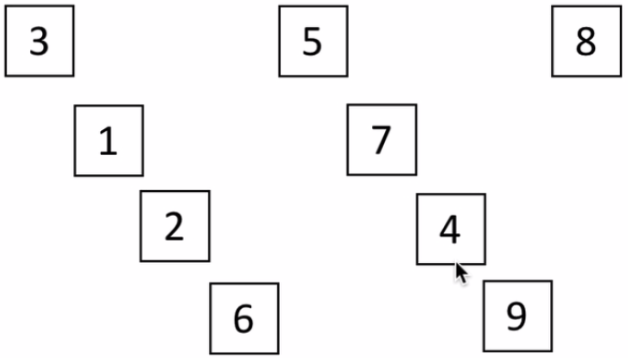
排序完成后,将这些元素返回列表:

(2)第二趟排序
取d2=d1/2,得到d2=2,将整个列表分为2组,每组相邻元素间距为2:
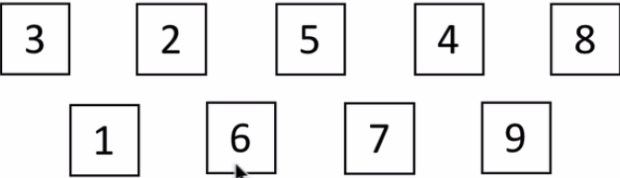
再在各个组内进行插入排序:
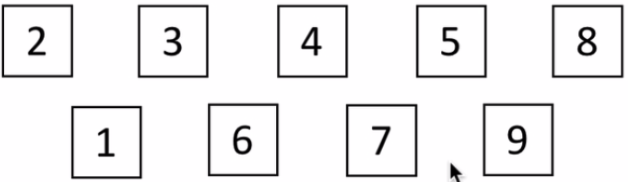
排序完成后,再将这些元素返回列表:

(3)最后一趟排序
此时d3=d2/2,得到d3=1,此时直接进行插入排序:

如此整个排序过程就完成了。希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序。
3、希尔排序代码实现
def insert_sort_gap(li, gap):
"""
希尔排序的分组进行插入排序
:param li:列表
:param gap:分组的d,将插入排序所有的1改为gap
:return:
"""
for i in range(gap, len(li)): # i表示摸到牌的下标
tmp = li[i] # 摸到的牌
j = i - gap # j指得是手里牌的下标(比摸到的牌小gap)
while li[j] > tmp and j >= 0: # 循环条件
li[j + gap] = li[j] # 如果手里的牌大于摸到的牌,将摸到的牌换为之前手里的牌
j -= gap # 手里的牌移动到摸到牌的位置
li[j + gap] = tmp # 将摸到的牌插入有序区
# print(li) # 打印每一趟排序过程
def shell_sort(li):
"""希尔排序"""
d = len(li) // 2 # 取到第一次循环的d值
while d >= 1: # 每次循环d/2,知道d=1的时候结束循环
insert_sort_gap(li, d)
d //= 2 # d整除2并赋值给d
li = list(range(100))
import random
random.shuffle(li)
shell_sort(li)
print(li)
在希尔排序的理解时,我们倾向于对于每一个分组,逐组进行处理,但在代码实现中,我们可以不用这么按部就班地处理完一组再调转回来处理下一组(这样还得加个for循环去处理分组)比如[5,7,4,6,3,1,2,9,8] ,首次增量设gap=length/2=4,则为4组[5,3,8] [7,1] [4,2] [6,9],实现时不用循环按组处理,我们可以从第gap个元素开始,逐个跨组处理。
4、测试希尔排序性能
from cal_time import *
import copy, random
def insert_sort_gap(li, gap):...
@cal_time
def shell_sort(li):
"""希尔排序"""
d = len(li) // 2 # 取到第一次循环的d值
while d >= 1: # 每次循环d/2,知道d=1的时候结束循环
insert_sort_gap(li, d)
d //= 2 # d整除2并赋值给d
from insert_sort import insert_sort
from heap_sort import *
li = list(range(10000))
random.shuffle(li)
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
li3 = copy.deepcopy(li)
shell_sort(li1)
insert_sort(li2)
"""
shell_sort running time: 0.05884504318237305 secs.
insert_sort running time: 4.995609283447266 secs.
"""
shell_sort(li1)
heap_sort(li3)
"""
shell_sort running time: 0.05833792686462402 secs.
heap_sort running time: 0.04569196701049805 secs.
"""
由此可见希尔排序的运行效率要远远大于插入排序,与堆排序(牛逼三人组中最慢)相比略慢一点。
5、希尔排序的时间复杂度
希尔排序的时间复杂度比较复杂,且与选择的gap(步长)序列有关。
只要最终步长为1任何步长序列都可以工作。算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序,最终算法以步长为1进行排序。当步长为1时,算法变为普通插入排序,这就保证了数据一定会被排序。
Donald Shell最初建议步长选择为n/2并且对步长取半直到步长达到1。虽然这样取可以比O(n2)类的算法(插入排序)更好,但这样仍然有减少平均时间和最差时间的余地。
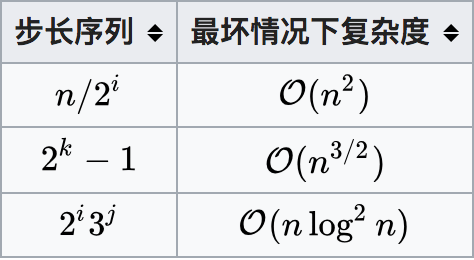
更多不同gap情况时间复杂度:https://en.wikipedia.org/wiki/Shellsort#Gap_sequences
二、计数排序
对列表进行排序,已知列表中的数范围都在0到100之间。设计时间复杂度为O(n)的算法。
统计每个数字出现了几次。
1、计数排序代码实现
def count_sort(li, max_count=100):
"""
计数排序
:param li:
:param max_count:
:return:
"""
count = [0 for _ in range(max_count+1)] # 生成一个值全为0长度为100+1的列表
for val in li: # 遍历li列表的值
count[val] += 1 # 值对应count列表下标,遍历到便执行加1
# 这样设计也限制了不能用大于100的数字进行排序,因为超出了index下标的范围
li.clear() # 列表清空
for ind, val in enumerate(count): # 下标、值
for i in range(val): # 遍历值(对应下标的统计次数)
li.append(ind) # 将下标值添加到li列表中(统计了几次就添加几次)
import random
li = [random.randint(0, 100) for _ in range(10)]
print(li)
count_sort(li)
print(li)
count[val] += 1是代码的精髓,不仅统计了对应值的出现次数,完成了排序,还限制了不能用大于下标范围的数字进行排序,如果超出下标返回,会提示报错。
2、计数排序和系统内置sort函数性能对比
from cal_time import *
@cal_time
def count_sort(li, max_count=100):
"""
计数排序
:param li:
:param max_count:
:return:
"""
count = [0 for _ in range(max_count+1)] # 生成一个值全为0长度为100+1的列表
for val in li: # 遍历li列表的值
count[val] += 1 # 值对应count列表下标,遍历到便执行加1
li.clear() # 列表清空
for ind, val in enumerate(count): # 下标、值
for i in range(val): # 遍历值(对应下标的统计次数)
li.append(ind) # 将下标值添加到li列表中(统计了几次就添加几次)
@cal_time
def sys_sort(li):
li.sort()
import random,copy
li = [random.randint(0, 100) for _ in range(100000)]
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
count_sort(li1)
sys_sort(li2)
"""
count_sort running time: 0.0277559757232666 secs.
sys_sort running time: 0.02849888801574707 secs.
"""
系统排序是用c语言写的,因此运行效率很高,在这里可以看到计数排序效率比系统排序还要高。
3、计数排序时间复杂度
对列表进行排序,已知列表中的数范围都在0到100之间。设计时间复杂度为O(n)的算法。0-100需要消耗一个长度是100的列。如果是一亿就要开一亿长的列。
常用于年龄等排序。此时不再往里面append值,而是append对象。
三、桶排序(Bucket Sort)
在计数排序中,如果遇到元素值的范围比较大(比如在1到1亿之间),是不适用的,改造算法就有桶排序。
桶排序:首先将元素分在不同的桶中,再对每个桶中的元素排序。
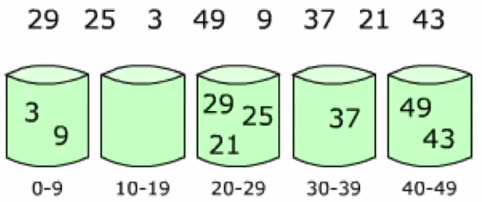
1、桶排序初步代码实现
def bucket_sort(li, n=100, max_num=10000):
"""
桶排序
:param li:
:param n: 桶的个数
:param max_num: 数字最大值
:return:
"""
buckets = [[] for _ in range(n)] # 创建桶:列表生成式生成二维列表,[[], [],...,[]]
for var in li: # 遍历列表所有数放在合适的桶里
# i = var // (max_num // n) # i表示var放到几号桶里86//(10000//100)=0,所以放在0号桶,但是处理不了10000
i = min(var // (max_num // n), n-1) # 为了解决10000这个数,将原i值和n-1=99作比较取小
buckets[i].append(var) # 将var放入对应的桶内
# 保持桶内的顺序(插入排序)
for j in range(len(buckets[i])-1, 0, -1): # 在列表[4,7,2,5]从后往前倒着取值
if buckets[i][j] < buckets[i][j-1]: # 如果后面的元素小于前一个元素就交换它
buckets[i][j], buckets[i][j-1] = buckets[i][j-1], buckets[i][j]
else:
break
# 将桶里的数输出出来
sorted_li = []
for buc in buckets: # buc是每一个桶
sorted_li.extend(buc)
return sorted_li
import random
li = [random.randint(0,10000) for i in range(100000)]
print(li)
li = bucket_sort(li)
print(li)
2、桶排序的性能
桶排序的表现取决于数据的分布,也就是需要对不同的数据排序时采取不同的分桶策略。
n是列表的长度,k是桶的个数。
平均情况事件复杂度:O(n+k),类似于线性的复杂度。
最坏情况时间复杂度:O(n2k),最坏情况下比O(n2)还要高。
空间复杂度:O(nk),占用了一个桶的空间,占用了O(nk)。
四、基数排序(radix sort)
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序。
1、多关键字排序
假如现在有一个员工表,要求按照薪资排序,薪资相同的员工按照年龄排序。
先按照年龄进行排序,再按照薪资进行稳定的排序。
对32,13,94,52,17,54,93排序,是否可以看作多关键字排序?可以,十位看作是第一关键字,个位看作是第二关键字。
2、图解多关键字排序
先按照个位分桶:
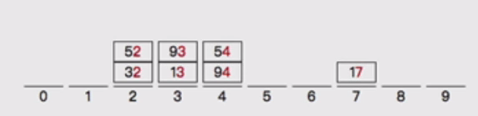
接下来依次输出每个桶的数据:

这样就实现了按个位数进行排序,满足了个位数小的一定在前面
接下来要按照十位数来分桶:

再次依次输出每个桶的数据:

3、基数排序代码实现
def radix_sort(li):
"""基数排序,装桶输出不做排序"""
max_num = max(li) # 最大值99->2, 888->3, 10000->5
it = 0
while 10 ** it <= max_num: # 如果10的it次方小于等于max_num,即满足循环条件
buckets = [[] for _ in range(10)] # 生成10个桶
for var in li:
"""
取数字个位数的值:987%10 取余
取数字十位数的值:(987//10)%10 取整再取余
取数字百位数的值:(987//100)%10 对100取整再取余
"""
digit = (var // 10 ** it) % 10
buckets[digit].append(var) # 分桶
# 分桶完成,将数据依次取出
li.clear()
for buc in buckets:
li.extend(buc) # 将数据重新写回li
it += 1
import random
li = list(range(1000))
random.shuffle(li)
radix_sort(li)
print(li)
分拆函数的写法:
def list_to_buckets(li, base, iteration):
"""
列表到桶
:param li:
:param base: 分的桶的个数
:param iteration: 装桶是第几次迭代
:return:
"""
buckets = [[] for _ in range(base)]
for number in li:
digit = (number // (base ** iteration)) % base
buckets[digit].append(number)
return buckets
def buckets_to_list(buckets):
return [x for bucket in buckets for x in bucket]
# li = []
# for bucket in buckets:
# for num in bucket:
# li.append(num)
def radix_sort(li, base=10):
maxval = max(li)
it = 0
while base ** it <= maxval:
li = buckets_to_list(list_to_buckets(li, base, it))
it += 1
return li
import random
li = [random.randint(0,100) for _ in range(10)]
random.shuffle(li)
s = radix_sort(li)
print(s) # [3, 10, 22, 27, 38, 43, 45, 54, 59, 72]
4、基数排序的特性和效率
时间复杂度:O(kn),这里的k = log10n,而快速排序是O(nlog2n)。由此可见基数排序比快排要快。但是当数字范围越来越大,k越来越大时,效率会慢于快排。
空间复杂度:O(k+n),基数排序空间上会消耗一个桶,空间消耗也是比较大的。因此最常用的还是快速排序和python自带的排序