一、AVL树
AVL树是一棵自平衡的二叉搜索树。
1、平衡因子
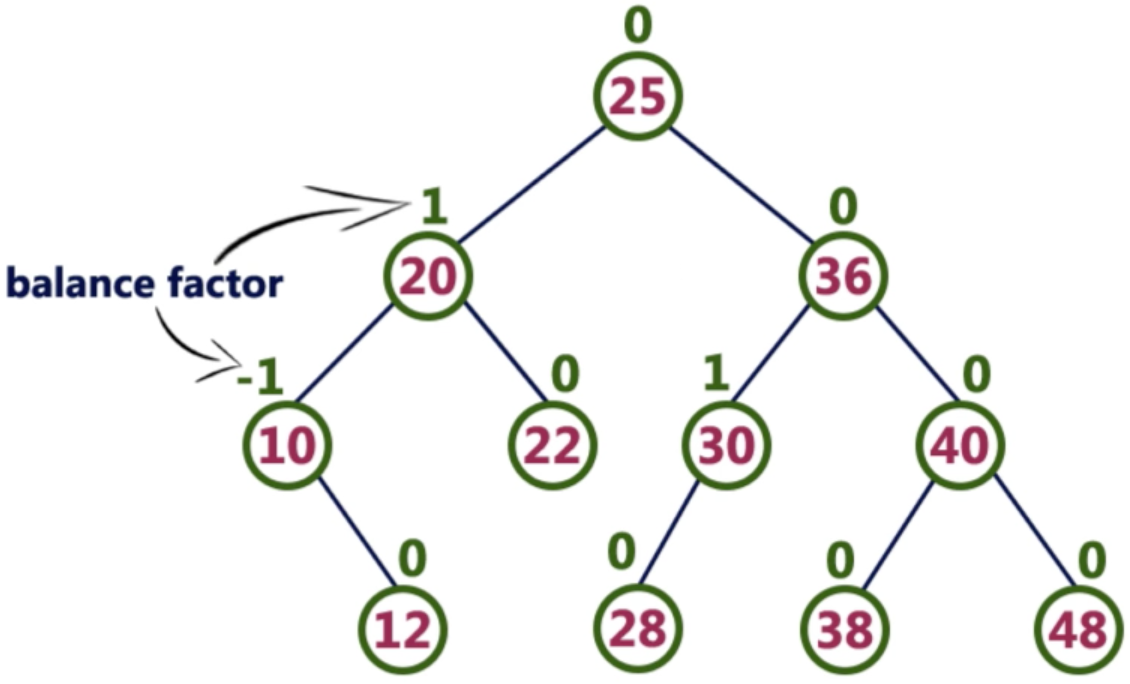
balance factor(平衡因子)记录了左右子树的高度差。上图定义的是有左子树没有右子树差值是1,没有左子树有右子树差值是-1.
2、AVL树具有以下性质
- 根的左右子树的高度之差的绝对值不能超过1
- 根的左右子树都是平衡二叉树(任何一个节点的左右子树高度差都不能超过1)
二、AVL树插入和旋转
插入一个节点可能会破坏AVL树的平衡,可以通过旋转操作来进行修正。
插入一个节点后,只有从插入节点到根节点的路径上的节点的平衡可能被改变。
我们需要找出第一个破坏了平衡条件的节点,称之为K。K的两颗子树的高度差为2。
1、不平衡的出现有4种情况
(1)不平衡是由于对K的右孩子的右子树插入导致的
操作方法:左旋
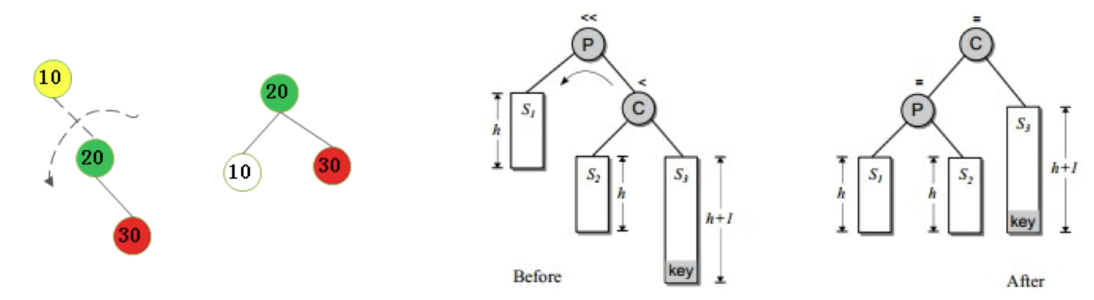
(2)不平衡是由于对K的左孩子的左子树插入导致的
操作方法:右旋
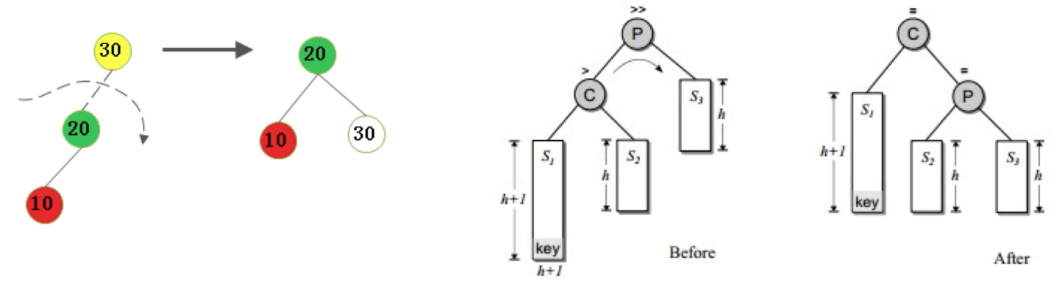
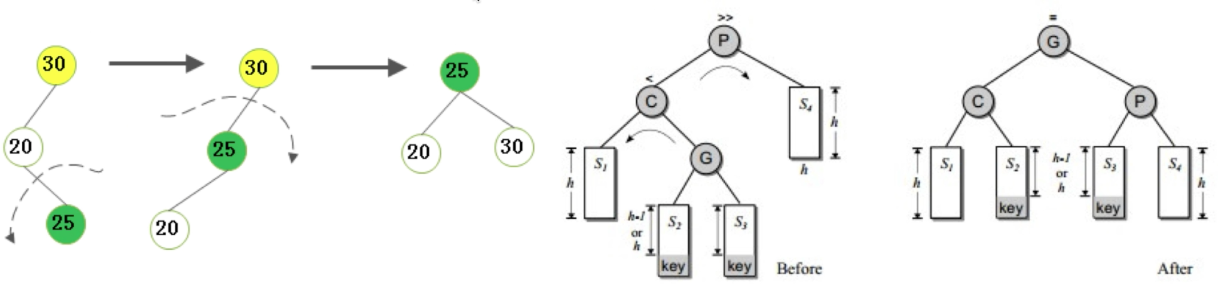
(3)不平衡是由于对K的右孩子的左子树插入导致的
操作方法:右旋——左旋
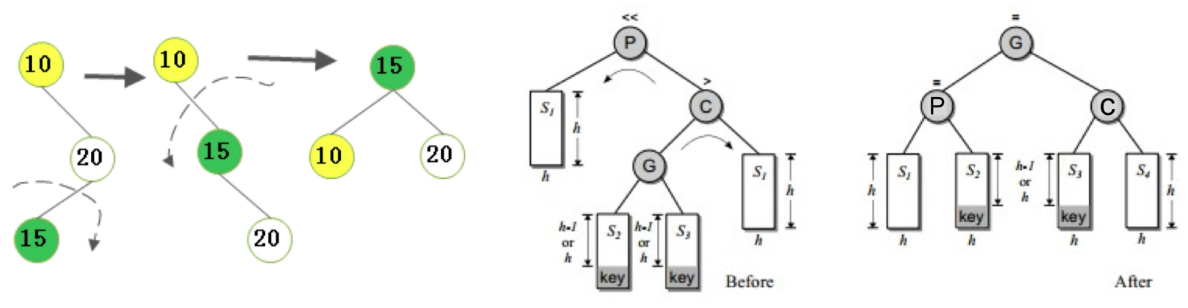
(4)不平衡是由于对K的左孩子的右子树插入导致的
操作方法:左旋——右旋
2、旋转代码实现
from .bst import BiTreeNode, BST
class AVLNode(BiTreeNode):
def __init__(self, data):
BiTreeNode.__init__(self, data)
self.bf = 0 # 平衡因子,bf=-1:左边树比右边高;bf=1:右边树比左边高
class AVLTree(BST):
def __init__(self, li=None):
BST.__init__(self, li)
def insert_no_rec(self, val):
"""重写插入方法"""
def rotate_left(self, p, c): # 根节点及其右孩子
"""对K的右孩子的右子树插入导致——左旋"""
s2 = c.lchild
p.rchild = s2
if s2: # 如果s2不为空
s2.parent = p
# C与P链接起来
c.lchild = p
p.parent = c
# 更新平衡因子
p.bf = 0
c.bf = 0
return c # 根节点
def rotate_right(self, p, c):
"""对K的左孩子的左子树插入导致——右旋"""
s2 = c.rchild
p.lchild = s2
if s2:
s2.parent = p
# C与P链接起来
c.rchild = p
p.parent = c
# 更新平衡因子
p.bf = 0
c.bf = 0
return c
def rotate_right_left(self, p, c):
"""由于对K的右孩子的左子树插入导致——右旋左旋"""
g = c.lchild # g节点是c的左孩子
# 右旋
s3 = g.rchild
c.lchild = s3 # c的左孩子绑定s3
if s3: # 如果s3存在
s3.parent = c # s3的父节点指向c(反链回去)
# G与C链接起来
g.rchild = c
c.parent = g
# 左旋
s2 = g.lchild
p.rchild = s2 # s2绑定给p的右孩子
if s2: # 如果s2存在
s2.parent = p
# G与P链接起来
g.lchild = p
p.parent = g
# 更新平衡因子
if g.bf > 0: # 插入的是s3,原G的右孩子
p.bf = -1 # p节点右边是空的
c.bf = 0
elif g.bf < 0: # 插入的是s2,原G的左孩子
p.bf = 0
c.bf = 1 # c节点左边是空的
else: # 插入的是G
p.bf = 0
c.bf = 0
def rotate_left_right(self, p, c):
"""由于对K的左孩子的右子树插入导致——左旋右旋"""
g = c.rchild # g节点是c的右孩子
# 左旋
s2 = g.lchild
c.rchild = s2 # c的右孩子绑定s2
if s2: # 如果s3存在
s2.parent = c # s2的父节点指向c(反链回去)
# G与C链接起来
g.lchild = c
c.parent = g
# 右旋
s3 = g.rchild
p.lchild = s3 # s3绑定给p的左孩子
if s3: # 如果s3存在
s3.parent = p
# G与P链接起来
g.rchild = p
p.parent = g
# 更新平衡因子
if g.bf < 0: # 插入的是s2,原G的左孩子
p.bf = 1
c.bf = 0
elif g.bf > 0: # 插入的是s3,原G的右孩子
p.bf = 0
c.bf = -1
else: # 插入的是G
p.bf = 0
c.bf = 0
3、根据AVL旋转实现AVL插入
from bst import BiTreeNode, BST
class AVLNode(BiTreeNode):
def __init__(self, data):
BiTreeNode.__init__(self, data)
self.bf = 0 # 平衡因子,bf=-1:左边树比右边高;bf=1:右边树比左边高
class AVLTree(BST):
def __init__(self, li=None):
BST.__init__(self, li)
def rotate_left(self, p, c): # 根节点及其右孩子
"""代码省略"""
def rotate_right(self, p, c):
"""代码省略"""
def rotate_right_left(self, p, c):
"""代码省略"""
def rotate_left_right(self, p, c):
"""代码省略"""
def insert_no_rec(self, val):
"""重写BST插入方法"""
# 1.第一步和BST一样做插入
p = self.root
if not p: # 空树的情况处理
self.root = AVLNode(val)
return
while True:
if val < p.data: # 添加值小于当前节点,往左边走
if p.lchild: # 如果左孩子存在
p = p.lchild
else: # 左子树不存在
p.lchild = AVLNode(val)
p.lchild.parent = p
node = p.lchild # node保存插入的节点
break
elif val > p.data: # 大于根节点往右边走
if p.rchild: # 如果右孩子存在
p = p.rchild
else: # 右子树不存在
p.rchild = AVLNode(val)
p.rchild.parent = p
node = p.rchild # node保存插入的节点
break
else: # 有一个一样值的节点,什么都不做
return
# 2.第二步更新平衡因子
while node.parent: # 如果node的父亲不是空
if node.parent.lchild == node: # 传递是从左子树来的,左子树更沉了
# 更新node.parent的平衡因子 -= 1
if node.parent.bf < 0: # 原来node.parent.bf==-1,更新后变为-2
# 做旋转
# 看node哪边沉
g = node.parent.parent # 用于连接旋转之后的子树
x = node.parent # 旋转前子树的根
if node.bf > 0: # node右边沉——》左右
n = self.rotate_left_right(node.parent, node)
else: # node左边沉——》左左
n = self.rotate_right(node.parent, node)
# 注意要将n和g连起来
elif node.parent.bf > 0: # 原来node.parent.bf==1,更新后变为0
node.parent.bf = 0
break
else: # 原来node.parent.bf == 0,更新后变为-1
node.parent.bf = -1
node = node.parent # 往上走一层继续循环
continue
else: # 传递是从右子树来的,右子树更沉了
# 更新node.parent.bf += 1
if node.parent.bf > 0: # 原来node.parent.bf==1,更新后变为2
# 做旋转
# 看node哪边沉
g = node.parent.parent # 用于连接旋转之后的子树
x = node.parent # 旋转前子树的根
if node.bf < 0: # node左边沉——》右左
n = self.rotate_right_left(node.parent, node)
else: # node右边沉——》右右
n = self.rotate_left(node.parent, node)
# 这里不考虑等于0的情况,因为传递上来了,肯定是因为它的bf不为0
# 记得连起来
elif node.parent.bf < 0: # 原来node.parent.bf==-1,更新后变为0
node.parent.bf = 0
break # 因为是0,就不需要传递了
else: # 原来node.parent.bf == 0,更新后变为1
node.parent.bf = 1
node = node.parent # 往上走一层继续循环
continue
# 链接旋转后的子树
n.parent = g
if g: # 如果g不是空
if x == g.lchild: # 如果旋转之前子树的根(x)是g的左孩子
g.lchild = n
else:
g.rchild = n
break
else: # 为空说明是根节点
self.root = n
break
tree = AVLTree([9,8,7,6,5,4,3,2,1])
tree.pre_order(tree.root)
print("")
tree.in_order(tree.root)
"""
6,4,2,1,3,5,8,7,9,
1,2,3,4,5,6,7,8,9,
"""