这个就念B树,不念B减树。
B-树(Balance Tree)是一种多路平衡查找树,一个m阶的B树具有如下几个特征:
1.根结点至少有两个子女。
2.每个中间节点都包含k-1个元素和k个孩子,其中 m/2 <= k <= m
3.每一个叶子节点都包含k-1个元素,其中 m/2 <= k <= m
4.所有的叶子结点都位于同一层。
5.每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划。
举例:对于一个3阶B树

插入操作:
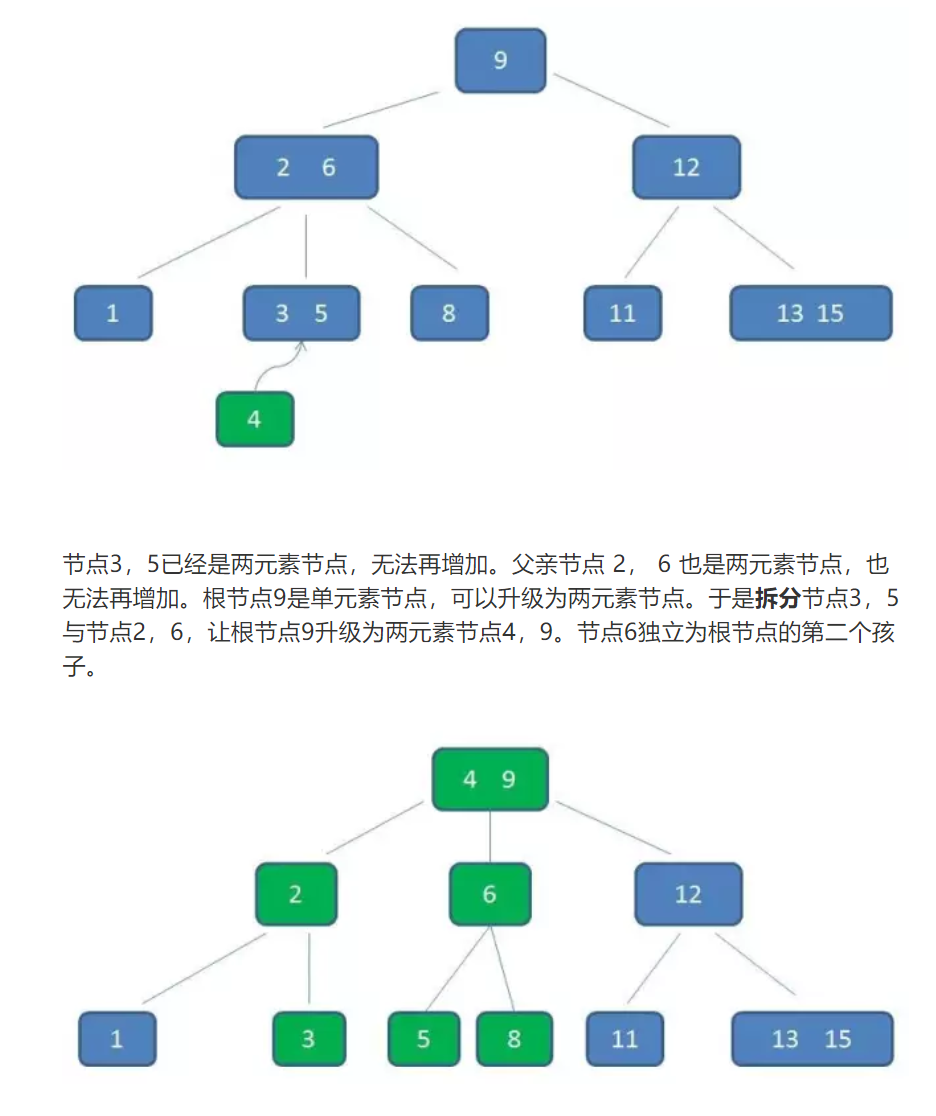
删除操作:
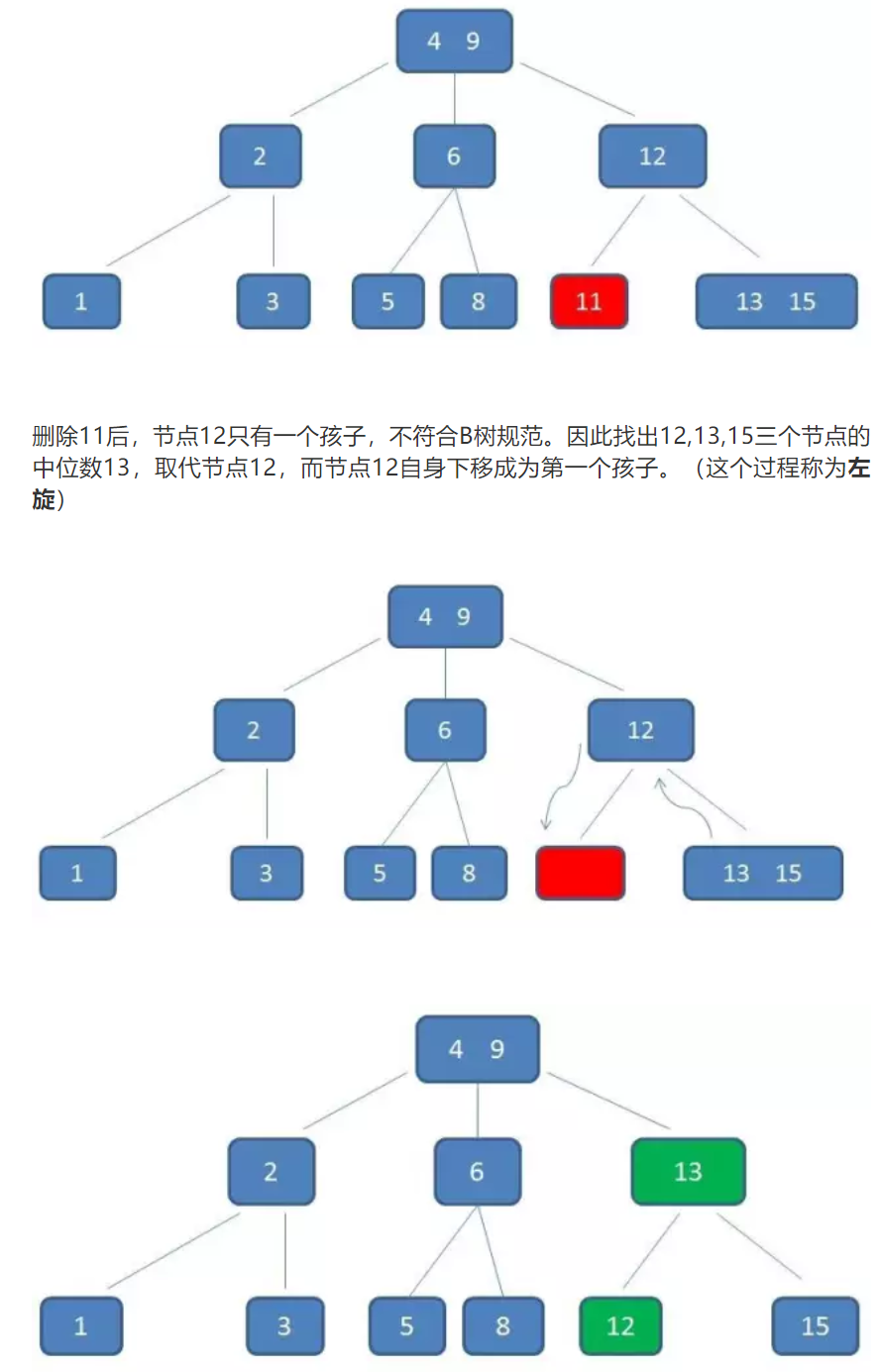
优势:算法上来说二叉查找树的查找速度和比较次数最小,但是对于数据库索引来说,还要考虑磁盘IO。磁盘IO的次数取决于索引树的深度。使用B树可以将索引树的深度减小。
B-树主要用于文件系统及部分数据库索引,比如非关系型数据库MongoDB。
一个 m 阶的 B + 树相较于B-树具有如下几个特征:
1. 有 k 个子树的中间节点包含有 k 个元素(B 树中是 k-1 个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
2. 所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
3. 所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。
另一种解释:
-
所有的数据都存储在叶子节点,中间节点不存放数据
-
中间节点的元素数量和子树数量一致,而B树子树数量比元素数量多1
-
叶子节点是一个链表,可以通过指针顺序查找
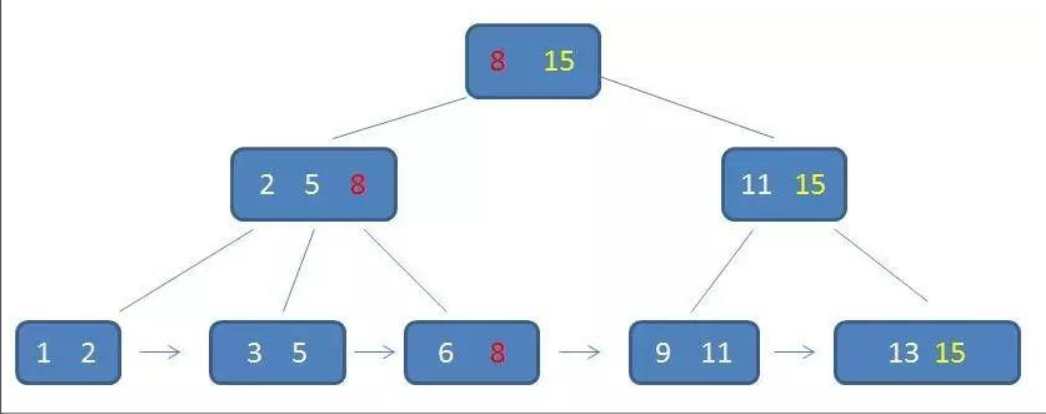
卫星数据:指索引元素所指向的数据记录
对比:
B - 树中的卫星数据(Satellite Information):

B + 树中的卫星数据(Satellite Information):

B+树的优势:
1.查询性能更好:相较于B树,B+树的中间节点没有卫星数据,同样大小的磁盘页可以容纳更多的节点数据。在数据量相同的情况下,IO次数更少。
2.查询性能更稳定:之前提到过,B+树的信息都保存在叶子节点,所以每次查找都必须到叶子节点为止,而B-树只用找到匹配元素即可,所以最好情况(根节点)和最坏情况(叶子节点)差距过大。
3.所有叶子节点形成有序链表,便于范围查询。
参考: