一.树
1.非线性结构,每个元素可以有多个前驱和后继
2.树是n(n>=0)个元素的集合
(1)n=0时,成为空树
(2)树只有一个特殊的没有前驱的元素,成为树的根Root
(3)树中除了根节点外,其余元素只能有一个前驱,可以有零个或多个后继
3.递归定义
(1)树T是n(n>=0)个元素的集合。n=0时,称为空树
(2)有且只有一个特殊元素根,剩余元素都可以被划分为m个互不相交的集合T1,T2,T3...Tm,而每一个集合都是数,称为T的子树Subtree
(3)子树也有自己的根
4.树的概念:如图
(1)结点:树中的数据元素称为结点
(2)结点的度degree:结点拥有的子树的数目称为度,记作d(v)。
(3)叶子结点:结点的度为0,称为叶子结点leaf,终端结点,末端结点
(4)分支结点:结点的度不为0,称为非终端结点或分支结点
(5)内部结点:除根结点外的分支结点,当然也不包括叶子结点
(6)树的度是树内各结点的度的最大值(D结点度最大为3,数的度数就是3):如图
(7)孩子(儿子Child)结点:结点的子树的根结点称为该结点的孩子(B是A的孩子)
(8)双亲(父Parent)结点:一个结点是它各子树的根结点的双亲(B和A是双亲结点)
(9)兄弟(Sibling)结点:居右相同双亲结点的结点(B和C,E和F是兄弟结点)
(10)祖先结点:从根结点到该结点所经分支上所有的结点(A,B,D都是G的祖先结点)
(11)子孙结点:结点的所有子树上的结点都称为该结点的子孙(B的子孙是D,G,H,I)
(12)结点的层次(Level):根结点为第一层,根的孩子为第二层,以此类推,记作L(v)
(13)树的深度(高度Depth):树的层次的最大值。上图的树深度为4
(14)堂兄弟:双亲在同一层的结点(D和E,D和F是堂兄弟)
(15)有序树:结点的子树是有序的(兄弟有大小,有先后次序)
(16)无序树:结点的子树是有无序的,可以交换
(17)路径:树中的k个结点n1,n2,...,nk,满足ni是n(i+1)的双亲,成为n1到nk的一条路径。就是一条线传下来的,前一个都是后一个的父(前驱)结点。
(18)路径长度=路径上节点数-1,也是分支树(上图路径长度是3)
(19)森林:m(m>=0)棵不相交的树的集合
对于结点而言,其子树的集合就是森林。A结点的2棵子树的集合就是森林
5.树的特点
(1)唯一的根
(2)子树不相交
(3)除了根以外,每个元素只能有一个前驱,可以有零个或多个后继
(4)根结点没有双亲结点(前驱),叶子结点没有孩子结点(后续)
(5)vi是vj的双亲,则L(vi)=L(vj)-1,也就是说双亲比孩子结点的层次小1
(6)堂兄弟的双亲不一定是兄弟关系
二.二叉树
1.每个结点最多2棵子树
(1)二叉树不存在度数大于2的结点
2.它是有序数,左子树,右子树是顺序的,不能交换次序
3.即使某个结点只有一颗子树,也要确定它是左子树还是右子树
4.二叉树的五种基本形态
(1)空二叉树
只有一个根结点
根结点只有左子树
根结点只有右子树
根结点有左子树和右子树
5.斜树(是二叉树)
(1)左斜树,所有结点都只有左子树
(2)右斜树,所有结点都只有右子树
6.满二叉树
(1)一颗二叉树的所有分支结点都存在左子树和右子树,并且有叶子结点只存在在最下面一层
(2)同样深度二叉树中,满二叉树结点最多。
(3)k为深度(1<=k<=n),则结点总数为2^k-1
(4)如图,一个深度为4的15个结点的满二叉树
7.完全二叉树(Complete Binary Tree)
(1)若二叉树的深度为k,二叉树的层数从1到k-1层的结点数都达到了最大个数,在第k层的所有结点都集中在左边,这就是完全二叉树
(2)完全二叉树由满二叉树引出
(3)满二叉树一定是完全二叉树,但完全二叉树不是满二叉树
(4)k为深度(1<=k<=n),则结点总数最大值为2^k-1,当达到最大值的时候就是满二叉树
(5)举例:
1)完全二叉树,最下一层的叶子结点都连续的集中在左边
2)不是完全二叉树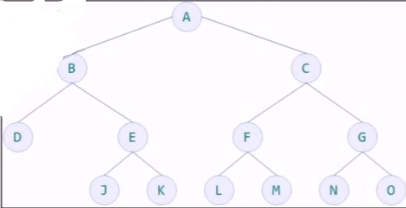
8.二叉树性质
性质1:
(1)在二叉树的第i层上至多有2^i-1个结点(i>=1)
性质2:
(1)深度为k的二叉树,至多有2^k-1个结点(k>=1)
(2)一层2-1=1
(3)二层4-1=1+2=3
(4)三层8-1=1+2+4=7
性质3:
(1)对任何一棵二叉树T,如果其终端节点数为n0,度数为2的结点为n2,则有n0=n2+1。换句话说,就是叶子结点数-1就等于度数为2的结点数
(2)证明:如图
度数为2的A,B
度数为1的C,E
度数为0的(叶子结点)D,G,F
1)总结点数为n=n0+n1+n2,n1为度数为1的结点总数。当前总结点为7
2)一棵树的分支数为n-1,因为除了根结点外,其余结点都有一个分支,即n0+n1+n2-1。当前分支为6
3)分支数还等于n0*0+n1*1+n2*2,n2是2分支结点所以乘以2,2*n2+n1。当前分支为6
4)可得2*n2+n1=n0+n1+n2-1=>n2=n0-1
其他性质:
(1)高度为k的二叉树,至少有k个结点
(2)含有n(n>=1)的结点的二叉树高度至多为n,和上一句一个意思
(3)含有n(n>=1)的结点的二叉树的高度至多为n,最小为math.ceil(log2(n+1)),不小于对数值的最小整数,向上取整。
假设高度为h,2^h-1=n=>h=log2(n+1),层次数是取整。如果是8个结点,3.1699就要向上取整为4,为4层
性质4:
具有n个结点的完全二叉树的深度为int(log2n)+1或者math.ceil(log2(n+1))
性质5:
(1)如果有一棵n个结点的完全二叉树(深度为性质4),结点按照层序编号,如图

(2)如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是int(i/2),向下取整。就是子结点的编号整除2得到的就是父结点的编号。父结点如果是i,那么左孩子结点就是2i,右孩子结点就是2i+1
(3)如果2i>n,则结点i无左孩子,即结点i为叶子结点;否则其左孩子结点存在编号为2i
(4)如果2i+1>n,则结点i无右孩子,注意这里并不能说明结点i没有左孩子;否则右孩子结点存在编号为2i+1.
三.树的遍历
1.二叉树的遍历
2.遍历:迭代所有元素一遍
3.书的遍历:对树中所有元素不重复地访问一遍,也称作扫描
4.广度优先遍历:
(1)层序遍历:
①按照书的层次,从第一层开始,自左向右遍历元素
②遍历序列:ABCDEFGHI,如图:

5.深度优先遍历
设树的根节点为D,左子树为L,右子树为R,且要求L一定在R之前,则有下面几种遍历方式
(1)前序遍历(前根遍历):DLR
①从根节点开始,先左子树后右子树
②每个子树内部依然是先根结点,再左子树后右子树,递归遍历
③遍历顺序:A BDGH CEIF ,如图:
(2)中序遍历(中根遍历):LDR
①从根结点的左子树开始遍历,然后是根结点,再右子树
②每个子树内部,也是先左子树,后根结点,再右子树。递归遍历
③遍历序列:GDHB A IECF ,如图
④遍历序列:GDHB A EICF ,如图
(3)后序遍历(后根遍历):LRD
①先左子树,后右子树,再根结点
②每个子树内部依然是先左子树,后右子树,再根结点,递归遍历
③遍历序列:GHDB IEFC A ,如图
6.遍历序列:将树中所有元素遍历一遍后,得到的元素的序列。将层次结构转换成了线性结构
四.堆排序Heap Sort
1.堆Heap
(1)堆是一个完全二叉树
(2)大顶堆:
①完全二叉树的每个非子结点都要大于或者等于其左右孩子结点的值称为大顶堆
②根结点一定是大顶堆中的最大值,如图

(3)小顶堆:
①完全二叉树的每个非叶子结点都要小于或者等于其左右孩子结点的值称为小顶堆
②根结点一定是小顶堆中的最小值,如图
(4)根结点一定是大顶堆中的最大值,一定是小顶堆中的最小值
2.堆排序Heap Sort
(1)构建完全二叉树
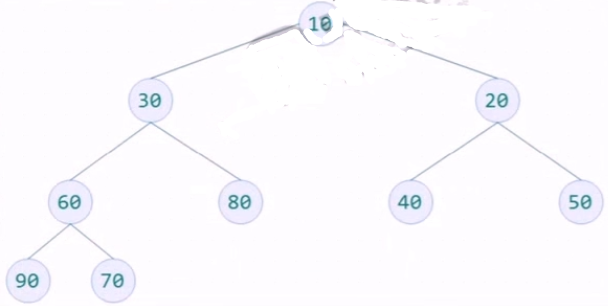
待排序数字为30,20,80,40,50,10,60,70,90
构建一个完全二叉树存放数据,并根据性质5对元素编号,放入顺序结构中
构造一个列表为[0,30,20,80,40,50,10,60,70,90]