Description
Solution
分层图最短路
模板题。
简单来说,就是将原图复制成 (k + 1) 份,从上面一层向下一层对应的节点(原图中向谁连边谁就是对应节点)连边,权值为 0(表示免费坐飞机)。
看图片理解吧,这是样例的解释图
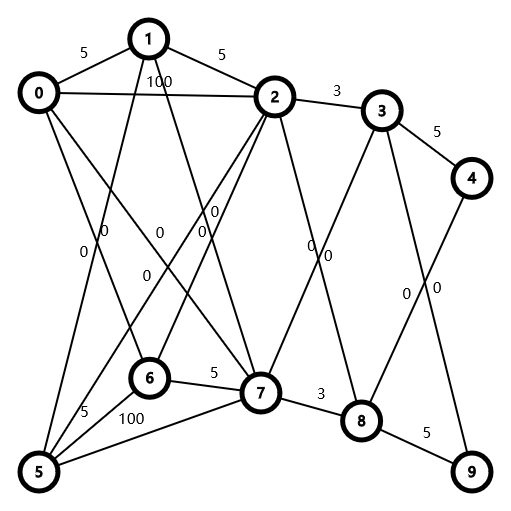
那么我们这道题基本就完成了。
但还有一个小坑。
可能用不到 (k) 次坐飞机的机会就能到达终点。
所以我们要在相邻两层的 (t) 节点连一条权值为 0 的节点。
Code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#define INF 0x3f3f3f3f
using namespace std;
const int N = 1e4 + 10;
const int M = 5e4 + 10;
typedef pair<int,int> P;
int n, m, k, s, t;
struct node{
int v, w, nxt;
}edge[M * 100];
int head[N * 15], tot;
int dis[N * 15];
void add(int x, int y, int z){
edge[++tot] = (node){y, z, head[x]};
head[x] = tot;
}
void dijkstra(int s){
priority_queue<P, vector<P>, greater<P> > q;
q.push(P(0, s));
memset(dis, INF, sizeof(dis));
dis[s] = 0;
while(!q.empty()){
P p = q.top();
q.pop();
int x = p.second;
if(dis[x] < p.first) continue;
for(int i = head[x]; i; i = edge[i].nxt){
int y = edge[i].v;
if(dis[y] > dis[x] + edge[i].w){
dis[y] = dis[x] + edge[i].w;
q.push(P(dis[y], y));
}
}
}
}
int main(){
scanf("%d%d%d%d%d", &n, &m, &k, &s ,&t);
for(int i = 1; i <= m; i++){
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
add(u, v, w), add(v, u, w);
for(int j = 1; j <= k; j++){ //分层图连边
add(u + (j - 1) * n, v + j * n, 0), add(u + j * n, v + j * n, w);
add(v + (j - 1) * n, u + j * n, 0), add(v + j * n, u + j * n, w);
}
}
for(int i = 1; i <= k; i++) //处理坑点
add(t + (i - 1) * n, t + i * n, 0);
dijkstra(s);
printf("%d
", dis[t + n * k]);
return 0;
}