Description
SOlution
题意非常清晰明了,下面我们来谈一谈如何求解。
实际上跟 P3391 是一样的,我们先考虑 \(i\) 和 \(j\) 都从 1 开始的情况,即:
\[\sum\limits_{i = 1}^n\sum\limits_{j = 1}^nlcm(a_i, a_j)
\]
直接求是不太行的,所以我们把输入的属放到一个桶里面,设为 \(t\)。
那么我们最终要求的答案就是:
\[\sum_{i=1}^n\sum_{j=1}^n lcm(i,j)\times t[i] \times t[j]
\]
下面就是喜闻乐见的推式子环节啦。
\[\sum_{i=1}^n\sum_{j=1}^n \frac{i \times j\times t[i] \times t[j]}{\gcd(i,j)}
\\
\sum_{i=1}^n\sum_{j=1}^n\sum\limits_{d = 1}^n\frac{i \times j\times t[i] \times t[j]}{[\gcd(i,j) == d]d}
\]
把 \(d\) 提前:
\[\sum_{d=1}^n\sum_{i=1}^{\lfloor \frac{n}{d} \rfloor}\sum_{j=1}^{\lfloor \frac{n}{d} \rfloor}\frac{id \times jd\times t[id] \times t[jd]}{[\gcd(i,j) == 1]d}
\]
上下同时除以 \(d\):
\[\sum_{d=1}^n\sum_{i=1}^{\lfloor \frac{n}{d} \rfloor}\sum_{j=1}^{\lfloor \frac{n}{d} \rfloor}[\gcd(i,j)=1]d\times i \times j \times t[id] \times t[jd]
\]
经典莫比乌斯反演:
\[\sum_{d=1}^n\sum_{i=1}^{\lfloor \frac{n}{d} \rfloor}\sum_{j=1}^{\lfloor \frac{n}{d} \rfloor}\sum_{k|(i,j)}\mu(k) \times d\times i \times j \times t[id] \times t[jd]
\]
把 \(k\) 提前:
\[\\
\sum_{d=1}^n\sum_{k=1}^{\lfloor \frac{n}{d}\rfloor}\sum_{i=1}^{\lfloor \frac{n}{kd}\rfloor}\sum_{j=1}^{\lfloor \frac{n}{kd}\rfloor}\mu(k)\times d \times i \times j \times k^2 \times t[idk] \times t[jdk]
\]
套路的令 \(T = dk\):
\[\\
\sum\limits_{T = 1}^n\sum\limits_{k | T}\sum_{i=1}^{\lfloor \frac{n}{T}\rfloor}\sum_{j=1}^{\lfloor \frac{n}{T}\rfloor}\mu(k)\times T \times k \times i \times j \times t[iT] \times t[jT]
\\
\sum_{T=1}^{n}T\times(\sum_{i=1}^{\lfloor \frac{n}{T} \rfloor}i\times t[iT])^2 \times \sum_{k|T}\mu(k)\times k
\]
至此,我们的式子就推完了,最后一项预处理,前面的暴力计算答案即可。
但是我们现在求的是 \(j\) 从 1 开始的情况,那从 \(i + 1\) 开始的话答案是多少呢?
也很简单,看一张图就明白了:
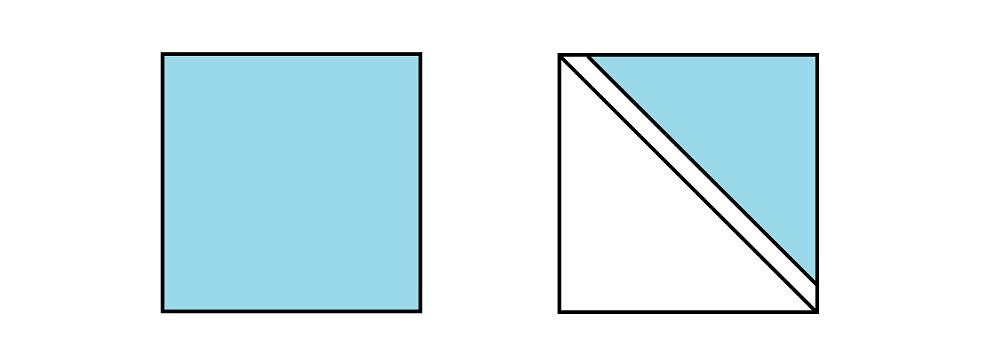
我们推的式子是第一个完整的正方形,而答案要求的是右边那个上三角。
所以我们减去对角线再除以二就是题目要求的答案了。
即:
\[ans = \frac{res - \sum\limits_{i = 1}^nlcm(a_i, a_i) }{2}
\]
\(res\) 是上面推的式子所求的值,显然要减去的 \(\sum\) 就是 \(a\) 数组的和。
Code
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace IO{
inline int read(){
int x = 0;
char ch = getchar();
while(!isdigit(ch)) ch = getchar();
while(isdigit(ch)) x = (x << 3) + (x << 1) + ch - '0', ch = getchar();
return x;
}
template <typename T> inline void write(T x){
if(x > 9) write(x / 10);
putchar(x % 10 + '0');
}
}
using namespace IO;
const int N = 5e4;
int n, m;
int t[N + 10], p[N + 10], mu[N + 10], tot;
ll sum[N + 10];
bool vis[N + 10];
inline void euler(int n){
mu[1] = 1;
for(int i = 2; i <= n; ++i){
if(!vis[i]) p[++tot] = i, mu[i] = -1;
for(int j = 1; j <= tot && i * p[j] <= n; ++j){
vis[i * p[j]] = 1;
if(i % p[j] != 0) mu[i * p[j]] = -mu[i];
else break;
}
}
for(int i = 1; i <= n; ++i)
for(int j = i; j <= n; j += i)
sum[j] += 1ll * mu[i] * i;
}
inline ll solve(int n){
ll ans = 0;
for(int T = 1; T <= n; ++T){
ll res = 0;
for(int i = 1; i <= n / T; ++i) res += 1ll * i * t[i * T];
ans += 1ll * T * res * res * sum[T];
}
return ans;
}
int main(){
n = read();
for(int i = 1, x; i <= n; ++i)
t[x = read()]++, m = max(m, x);
euler(m);
write(solve(m)), puts("");
return 0;
}
\[\_EOF\_
\]