首先得明确逻辑回归与线性回归不同,它是一种分类模型。而且是一种二分类模型。
首先我们需要知道sigmoid函数,其公式表达如下:
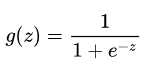
其函数曲线如下:
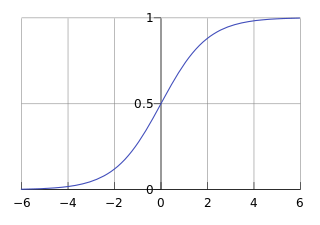
sigmoid函数有什么性质呢?
1、关于(0,0.5) 对称
2、值域范围在(0,1)之间
3、单调递增
4、光滑
5、中间较陡,两侧较平缓
6、其导数为g(z)(1-g(z)),即可以用原函数直接计算
于是逻辑回归的函数形式可以用以下公式表示:

其中θ表示权重参数,x表示输入。θTx为决策边界,就是该决策边界将不同类数据区分开来。
为什么使用sigmoid函数呢?
1、sigmoid函数本身的性质
2、推导而来
我们知道伯努利分布:
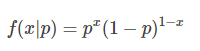
当x=1时,f(1|p) =p,当x=0时,f(0|p)=1-p
首先要明确伯努利分布也是指数族,指数族的一般表达式为:

由于:
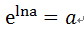
则有:

所以:
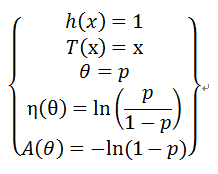
因为:
 则有:
则有:
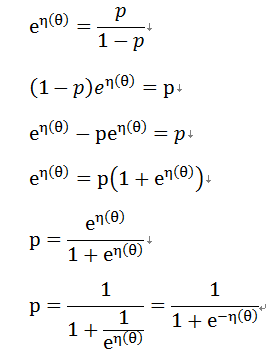
逻辑回归代价函数:

为什么这么定义呢?
以单个样本为例:

上面式子等价于:
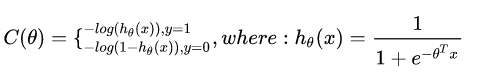
当y=1时,其图像如下:
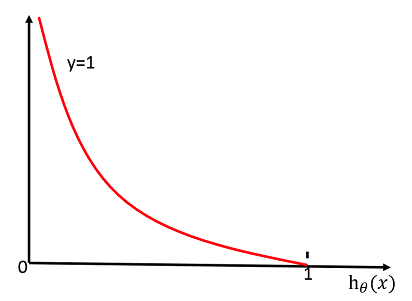
也就是说当hθ(x)的值越接近1,C(θ) 的值就越小。
同理当y=0时,其图像如下:
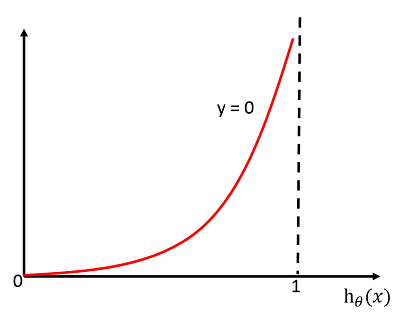
也就是说当hθ(x)的值越接近0,C(θ) 的值就越小。
这样就可以将不同类区分开来。
代价函数的倒数如下:
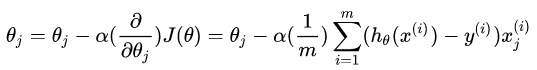
推导过程如下:
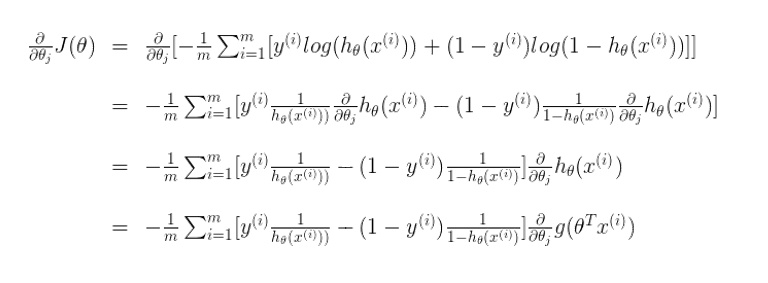
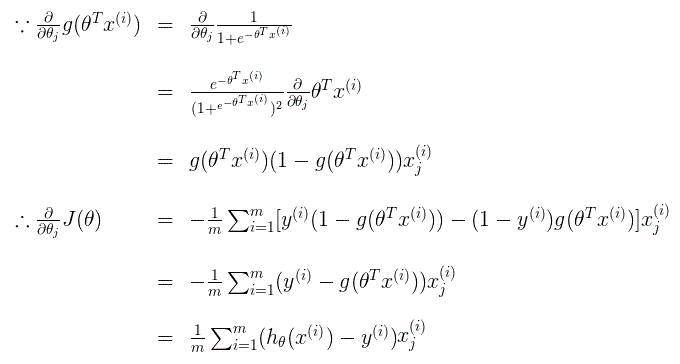
上面参考了:
https://blog.csdn.net/sun_wangdong/article/details/80780368
https://zhuanlan.zhihu.com/p/28415991
接下来就是代码实现了,代码来源: https://github.com/eriklindernoren/ML-From-Scratch
from __future__ import print_function, division import numpy as np import math from mlfromscratch.utils import make_diagonal, Plot from mlfromscratch.deep_learning.activation_functions import Sigmoid class LogisticRegression(): """ Logistic Regression classifier. Parameters: ----------- learning_rate: float The step length that will be taken when following the negative gradient during training. gradient_descent: boolean True or false depending if gradient descent should be used when training. If false then we use batch optimization by least squares. """ def __init__(self, learning_rate=.1, gradient_descent=True): self.param = None self.learning_rate = learning_rate self.gradient_descent = gradient_descent self.sigmoid = Sigmoid() def _initialize_parameters(self, X): n_features = np.shape(X)[1] # Initialize parameters between [-1/sqrt(N), 1/sqrt(N)] limit = 1 / math.sqrt(n_features) self.param = np.random.uniform(-limit, limit, (n_features,)) def fit(self, X, y, n_iterations=4000): self._initialize_parameters(X) # Tune parameters for n iterations for i in range(n_iterations): # Make a new prediction y_pred = self.sigmoid(X.dot(self.param)) if self.gradient_descent: # Move against the gradient of the loss function with # respect to the parameters to minimize the loss self.param -= self.learning_rate * -(y - y_pred).dot(X) else: # Make a diagonal matrix of the sigmoid gradient column vector diag_gradient = make_diagonal(self.sigmoid.gradient(X.dot(self.param))) # Batch opt: self.param = np.linalg.pinv(X.T.dot(diag_gradient).dot(X)).dot(X.T).dot(diag_gradient.dot(X).dot(self.param) + y - y_pred) def predict(self, X): y_pred = np.round(self.sigmoid(X.dot(self.param))).astype(int) return y_pred
说明:np.linalg.pinv()用于计算矩阵的pseudo-inverse(伪逆)。第一种方法求解使用随机梯度下降。
其中make_diagonal()函数如下:用于将向量转换为对角矩阵
def make_diagonal(x): """ Converts a vector into an diagonal matrix """ m = np.zeros((len(x), len(x))) for i in range(len(m[0])): m[i, i] = x[i] return m
其中Sigmoid代码如下:
class Sigmoid(): def __call__(self, x): return 1 / (1 + np.exp(-x)) def gradient(self, x): return self.__call__(x) * (1 - self.__call__(x))
最后是主函数运行代码:
from __future__ import print_function from sklearn import datasets import numpy as np import matplotlib.pyplot as plt # Import helper functions import sys sys.path.append("/content/drive/My Drive/learn/ML-From-Scratch/") from mlfromscratch.utils import make_diagonal, normalize, train_test_split, accuracy_score from mlfromscratch.deep_learning.activation_functions import Sigmoid from mlfromscratch.utils import Plot from mlfromscratch.supervised_learning import LogisticRegression def main(): # Load dataset data = datasets.load_iris() X = normalize(data.data[data.target != 0]) y = data.target[data.target != 0] y[y == 1] = 0 y[y == 2] = 1 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, seed=1) clf = LogisticRegression(gradient_descent=True) clf.fit(X_train, y_train) y_pred = clf.predict(X_test) accuracy = accuracy_score(y_test, y_pred) print ("Accuracy:", accuracy) # Reduce dimension to two using PCA and plot the results Plot().plot_in_2d(X_test, y_pred, title="Logistic Regression", accuracy=accuracy) if __name__ == "__main__": main()
结果:
Accuracy: 0.9393939393939394
