【python opencv】轮廓特征

1、特征矩

特征矩可以帮助您计算一些特征，例如物体的质心，物体的面积等。

函数cv.moments()提供了所有计算出的矩值的字典：

import numpy as np
import cv2 as cv
img = cv.imread('star.jpg',0)
ret,thresh = cv.threshold(img,127,255,0)
contours,hierarchy = cv.findContours(thresh, 1, 2)
cnt = contours[0]
M = cv.moments(cnt)
print( M )

{'m00': 33499.0,
 'm01': 8793702.666666666,
 'm02': 2409403646.833333,
 'm03': 685511505862.8,
 'm10': 8384054.0,
 'm11': 2200871350.6666665,
 'm12': 603023656059.5,
 'm20': 2199493589.5,
 'm21': 577381344709.9333,
 'm30': 601117677270.0,
 'mu02': 101000214.2013011,
 'mu03': 1162863.115234375,
 'mu11': 3324.239688873291,
 'mu12': 1812195.5510406494,
 'mu20': 101151505.41044497,
 'mu21': -1514017.5661506653,
 'mu30': 1453081.0164794922,
 'nu02': 0.09000333645341069,
 'nu03': 5.661727831836976e-06,
 'nu11': 2.962297313282231e-06,
 'nu12': 8.823186369609854e-06,
 'nu20': 0.09013815511401155,
 'nu21': -7.371422551688403e-06,
 'nu30': 7.07473573212249e-06}

从这一刻起，您可以提取有用的数据，例如面积，质心等。质心由关系给出，$C_x = frac{M_{10}}{M_{00}}$ 和 $C_y = frac{M_{01}}{M_{00}}$。可以按照以下步骤进行：

cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])

250

262

2、轮廓面积

轮廓区域由函数cv.contourArea()或从矩M['m00']中给出。

area = cv.contourArea(cnt) 

3、轮廓周长

也称为弧长。可以使用cv.arcLength()函数找到它。第二个参数指定形状是闭合轮廓(True)还是曲线。

perimeter = cv.arcLength(cnt,True)

4、轮廓近似

根据我们指定的精度，它可以将轮廓形状近似为顶点数量较少的其他形状。它是Douglas-Peucker算法的实现。

为了理解这一点，假设您试图在图像中找到一个正方形，但是由于图像中的某些问题，您没有得到一个完美的正方形，而是一个“坏形状”（如下图所示）。现在，您可以使用此功能来近似形状。在这种情况下，第二个参数称为epsilon，它是从轮廓到近似轮廓的最大距离。它是一个精度参数。需要正确选择epsilon才能获得正确的输出。

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
from google.colab.patches import cv2_imshow
img=cv.imread('轮廓近似.jpg',0)

ret,thresh = cv.threshold(img,127,255,0)
contours,hierarchy = cv.findContours(thresh, 1, 2)
cnt = contours[0]

epsilon = 0.1*cv.arcLength(cnt,True) 
approx = cv.approxPolyDP(cnt,epsilon,True)
print(approx)
image = cv.cvtColor(img, cv.COLOR_GRAY2BGR)
cv.polylines(image, [approx], True, (255, 0, 0), 2)

[[[ 11 14]] [[ 11 137]] [[194 137]] [[194 14]]]

我们将0.1改为0.01：

[[[ 11 14]] [[ 11 48]] [[ 26 54]] [[ 11 56]] [[ 11 112]] [[ 47 102]] [[ 13 120]] [[ 11 137]] [[ 78 137]] [[ 98 100]] [[119 137]] [[194 137]] [[194 85]] [[174 84]] [[194 77]] [[194 14]] [[171 14]] [[153 41]] [[161 14]] [[ 62 14]] [[ 65 37]] [[ 54 14]]]

5、轮廓凸包

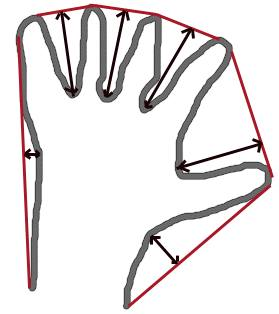
凸包外观看起来与轮廓逼近相似，但不相似（在某些情况下两者可能提供相同的结果）。在这里，cv.convexHull()函数检查曲线是否存在凸凹缺陷并对其进行校正。一般而言，凸曲线是始终凸出或至少平坦的曲线。如果在内部凸出，则称为凸度缺陷。例如，检查下面的手的图像。红线显示手的凸包。双向箭头标记显示凸度缺陷，这是凸包与轮廓线之间的局部最大偏差。

关于它的语法，有一些需要讨论：

hull = cv.convexHull(points[, hull[, clockwise[, returnPoints]] 

参数详细信息： - 点是我们传递到的轮廓。 - 凸包是输出，通常我们忽略它。 - 顺时针方向：方向标记。如果为True，则输出凸包为顺时针方向。否则，其方向为逆时针方向。 - returnPoints：默认情况下为True。然后返回凸包的坐标。如果为False，则返回与凸包点相对应的轮廓点的索引。

因此，要获得如上图所示的凸包，以下内容就足够了：

hull = cv.convexHull(cnt) 

但是，如果要查找凸度缺陷，则需要传递returnPoints = False。为了理解它，我们将拍摄上面的矩形图像。首先，我发现它的轮廓为cnt。现在，我发现它的带有returnPoints = True的凸包，得到以下值：[[[234 202]]，[[51 202]]，[[51 79]]，[[234 79]]]，它们是四个角 矩形的点。现在，如果对returnPoints = False执行相同的操作，则会得到以下结果：[[129]，[67]，[0]，[142]]。这些是轮廓中相应点的索引。例如，检查第一个值：cnt [129] = [[234，202]]与第一个结果相同（对于其他结果依此类推）。

6、检查凸度

cv.isContourConvex()具有检查曲线是否凸出的功能。它只是返回True还是False。没什么大不了的。

k = cv.isContourConvex(cnt) 

7、边界矩形

有两种类型的边界矩形。

（1）直角矩形

它是一个矩形，不考虑物体的旋转。所以边界矩形的面积不是最小的。它是由函数cv.boundingRect()找到的。

令(x，y)为矩形的左上角坐标，而(w，h)为矩形的宽度和高度。

x,y,w,h = cv.boundingRect(cnt)
cv.rectangle(img,(x,y),(x+w,y+h),(0,255,0),2)

（2）旋转矩形

这里，边界矩形是用最小面积绘制的，所以它也考虑了旋转。使用的函数是cv.minAreaRect()。它返回一个Box2D结构，其中包含以下细节 -(中心(x,y)，(宽度，高度)，旋转角度)。但要画出这个矩形，我们需要矩形的四个角。它由函数cv.boxPoints()获得

rect = cv.minAreaRect(cnt)
box = cv.boxPoints(rect)
box = np.int0(box)
cv.drawContours(img,[box],0,(0,0,255),2)

两个矩形都显示在一张单独的图像中。绿色矩形显示正常的边界矩形。红色矩形是旋转后的矩形。

8、最小闭合圈

接下来，使用函数*cv.minEnclosingCircle(()查找对象的圆周。它是一个以最小面积完全覆盖物体的圆。

(x,y),radius = cv.minEnclosingCircle(cnt)
center = (int(x),int(y))
radius = int(radius)
cv.circle(img,center,radius,(0,255,0),2)

9、拟合一个椭圆

下一个是把一个椭圆拟合到一个物体上。它返回内接椭圆的旋转矩形。

ellipse = cv.fitEllipse(cnt)
cv.ellipse(img,ellipse,(0,255,0),2)

10、拟合直线

rows,cols = img.shape[:2]
[vx,vy,x,y] = cv.fitLine(cnt, cv.DIST_L2,0,0.01,0.01)
lefty = int((-x*vy/vx) + y)
righty = int(((cols-x)*vy/vx)+y)
cv.line(img,(cols-1,righty),(0,lefty),(0,255,0),2)

参考：

http://woshicver.com/FifthSection/4_9_2_%E8%BD%AE%E5%BB%93%E7%89%B9%E5%BE%81/