[GWCTF 2019]xxor
步骤:
-
无壳,64位ida载入
-
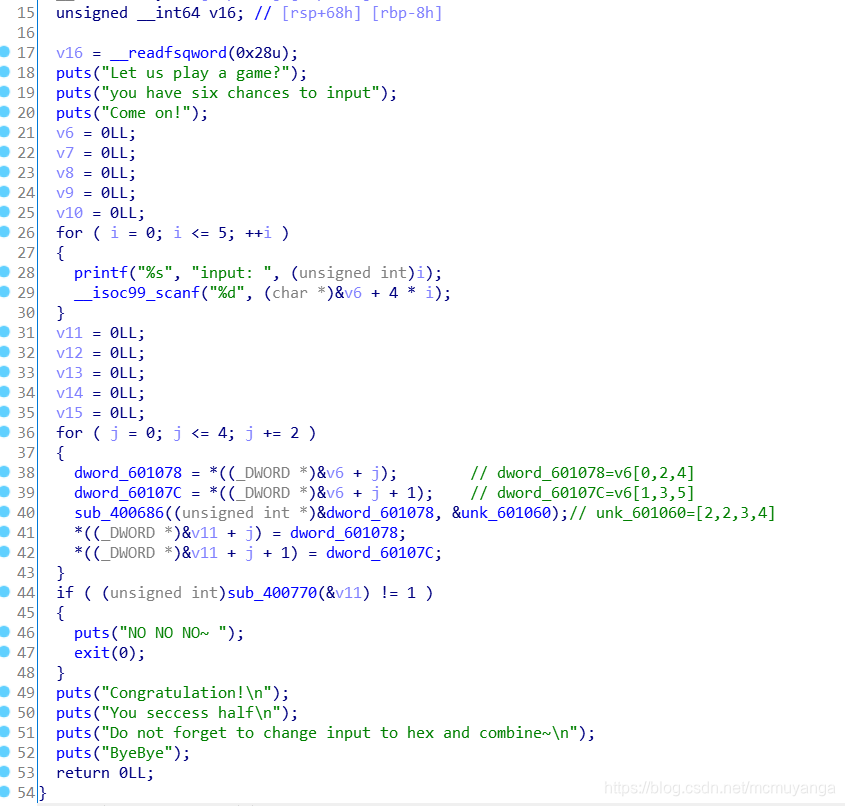
程序很简单,首先让我们输入一个字符串,然后进行中间部分的操作,最后需要满足44行的if判断,看一下sub_400770函数
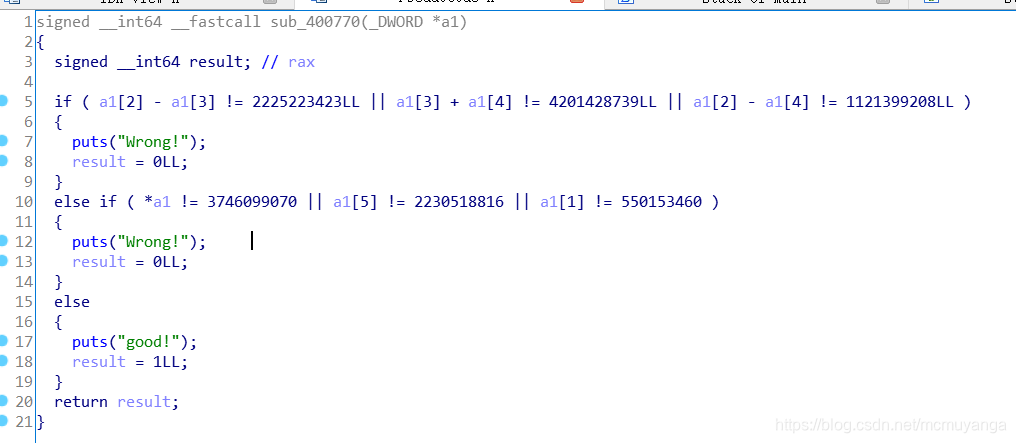
得到几个关系式
a1[2] - a1[3] = 2225223423
a1[3] + a1[4] = 4201428739
a1[2] - a1[4] = 1121399208
a1[0] = 3746099070
a1[5] = 550153460
a1[1] = 550153460
利用z3求解器求一下这几个值
我的python3.7安装z3库的指令python -m pip install z3-solver
from z3 import *
a2,a3,a4 = BitVecs('a2 a3 a4',64)
s = Solver()
s.add(a2 - a3 == 2225223423)
s.add(a3 + a4 == 4201428739)
s.add(a2 - a4 == 1121399208)
if s.check() == sat:
m = s.model()
for i in m:
print("%s = %ld" % (i, m[i].as_long()))

现在我们的a1数组里的值就都知道了a1=[3746099070, 550153460, 3774025685, 1548802262, 2652626477, 2230518816]
关于代码里的一些函数用法,看这篇介绍z3的文章
- 程序在main函数的36~43行进行了操作,看一下sub_400686函数
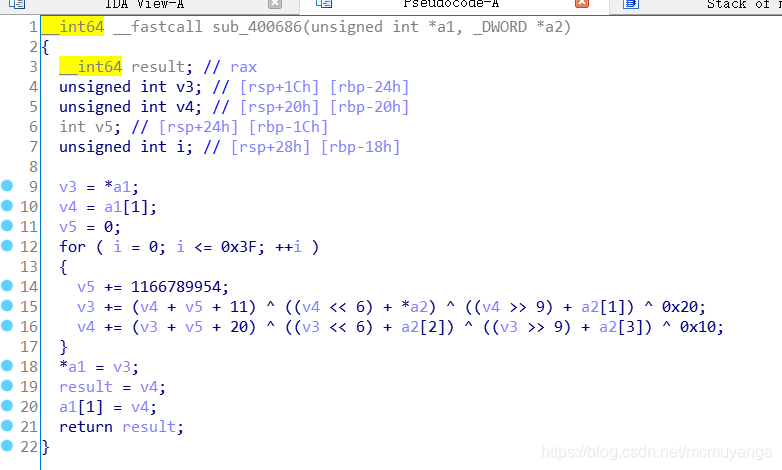
- 上述代码将我们输入的字符串进行了变换,形成了v11数组,也就是sub_400770的参数,这个值我们已经知道了,我们可以将这个进行操作的算法进行逆运算
本人用python去写逆算法太菜了,弄了一大堆报错,没办法了,直接将伪代码复制到c中修改
#include <stdio.h>
int main()
{
unsigned int a[6] = { 3746099070, 550153460, 3774025685, 1548802262, 2652626477, 2230518816 };
unsigned int a2[4] = { 2,2,3,4 };
unsigned int v3, v4;
int v5;
for (int j = 0; j <= 4; j += 2) {
v3 = a[j];
v4 = a[j + 1];
v5 = 1166789954 * 64;
for (int i = 0; i <= 0x3F; ++i) {
v4 -= (v3 + v5 + 20) ^ ((v3 << 6) + a2[2]) ^ ((v3 >> 9) + a2[3]) ^ 0x10;
v3 -= (v4 + v5 + 11) ^ ((v4 << 6) + *a2) ^ ((v4 >> 9) + a2[1]) ^ 0x20;
v5 -= 1166789954;
}
a[j] = v3;
a[j + 1] = v4;
}
for (int i = 0; i < 6; ++i)
/*将整型数组作为字符输出,注意计算机小端排序*/
printf("%c%c%c", *((char*)&a[i] + 2), *((char*)&a[i] + 1), *(char*)&a[i]);
}
