算法图解学习笔记01：二分查找&大O表示法

二分查找

　　二分查找又称折半查找，其输入的必须是有序的元素列表。二分查找的基本思想是将n个元素分成大致相等的两部分，取a[n/2]与x做比较，如果x=a[n/2],则找到x,算法中止；如果x<a[n/2],则只要在数组a的左半部分继续搜索x,如果x>a[n/2],则只要在数组a的右半部搜索x

　　

#python实现二分查找
def binary_search(list,item):
    low=0
    high=len(list)-1
    while(low<=high):
        mid=int((low+high)/2)
        if list[mid]==item:
            return mid
        if list[mid]>item:
            high=mid-1
        if list[mid]<item:
            low=mid+1
    return None

my_list=[1,2,4,8,9,15,22,30]
print(binary_search(my_list,2))

1

2

3

4

5

...

17

18

19

20

　　假设如上表1-20按顺序排序，采用二分查找方式查找。最好情况下查找1-20的mid即10，一次即可查找到。

　　如果是查找17呢？（这是最坏情况下）

　　第一趟，mid=10,17>mid，即low的下标变为mid+1=11，查找右半部分

　　

11

12

...

19

20

　　第二趟，mid变为（11+20）/2=15，17>mid，low的下标变为16，再次取上表的右半部,取上表左半部分

　　

16

17

18

19

20

　　第三趟，mid变为（16+20）/2=18,17<18，这次需要high的下标变为17

16

17

　　第四趟，mid变为（16+17）/2=16,17>16，这次需要low的下标变为17，此时low和high的下标均变为17

17

　　第五趟，mid=item=17，程序结束。程序共执行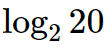次

 大O表示法

　　大O表示法是一种特殊的表示法，指出了算法的运行速度有多快。大O表示法指出了最糟情况下的运行时间。

• O(log n)，也叫对数时间，这样的算法包括二分查找。
• O(n)，也叫线性时间，这样的算法包括简单查找。
• O(n * log n)，这样的算法包括第4章将介绍的快速排序——一种速度较快的排序算法。
• O(n 2 )，这样的算法包括选择排序——一种速度较慢的排序算法。
• O(n!)，这样的算法包括接下来将介绍的旅行商问题的解决方案——一种非常慢的算法