目录
1.引子
2.什么是前缀树
3.如何实现前缀树
4.高级用法
引子
嗯,先随便造一个海量问题。给你一个大文件,里面有10 亿个英文字母序列,每个长度不超过255,需要你对这些数据建模。之后随便丢一些字母序列给你,让你快速回应,判断给定的字符序列是否在上面给定的那个大文件中出现过。
现在假设你是一个初入门径的Programmer,没有海量问题相关的实战经验,以现有的知识储备你会怎么解决这个问题?
- 全部读到内存,放到一个链表/数组里,随后一遍又一遍地遍历它,以O(N) 的时间查询某个字符序列?
- 存到哈希表,然后屁颠屁颠的号称以O(1) 的时间完美解决查询慢的问题?
不好意思,上面的搞法,在小数据规模上是完全够用的解决方案。但是放到这里,这么搞,不是时间复杂度过高,就是空间复杂度过高,中奖的话,还会出现时空双高爽飞你。查个数据查几分钟,内存也不见得放得下这么大的数据量,即便放下了,后面文件又追加了内容,同样的程序再次跑,还面临内存爆炸的风险,除非不想要你的饭碗了,否则为了一个好算法还是得殚精竭虑地费心思索一番。
不过,我们遇到的绝大多数问题,踩过的坑,前人已经遇到过并且踩实了。很多时候,不需要我们发明创造新的算法,学习下前人的奇技淫巧又够用了,真是幸福啊:-
呐,现在你Google 一个问题,如下图:
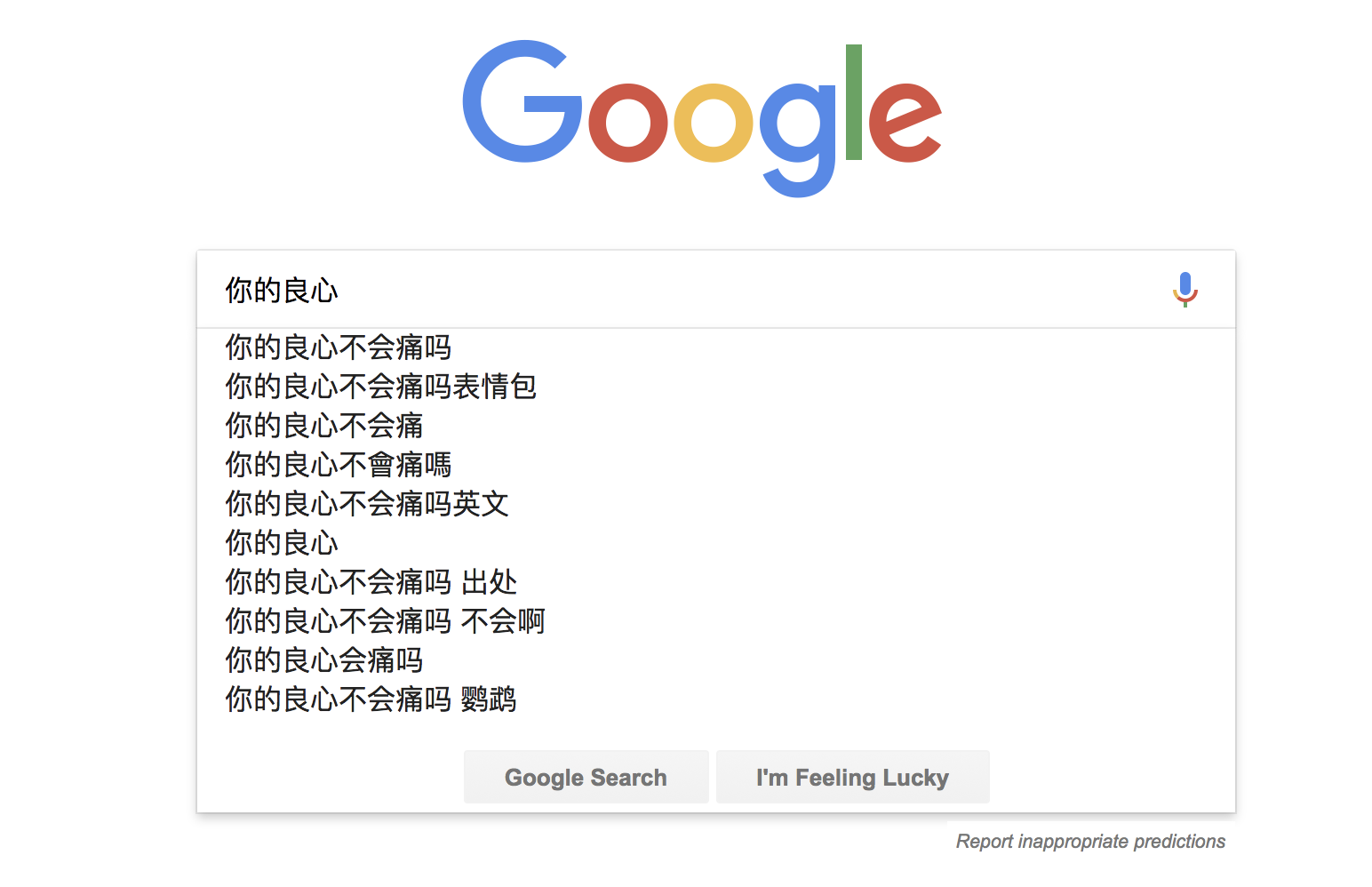
看看,是不是和我们待解决的问题结构很相似?很明显,Google 背后存储的搜索记录无疑是海量的,然后它还可以给出部分前缀匹配结果,也和我们待解决的问题相似,只不过我们要实现精确匹配而已。
作为一个技术人员,在你的好奇心和解决问题的急迫心情的驱使下,继续搜索“搜索引擎 搜索提示 技术原理” 就是顺其自然的事情了,当然了,用好搜索引擎除了不用baidu 搜索技术问题外,还是尽可能的直接用英文去检索资料,那是一片更加广阔的天地 ...
什么是前缀树
检索的过程中,你会发现有“Trie Tree” 这个神奇的数据结构的存在,也就是这里要说的前缀树——这个问题的一种解决方案。
这里我只是简单地以白话的方式,总结性的概括介绍下,更详细的内容可以去Wikipedia 看看。
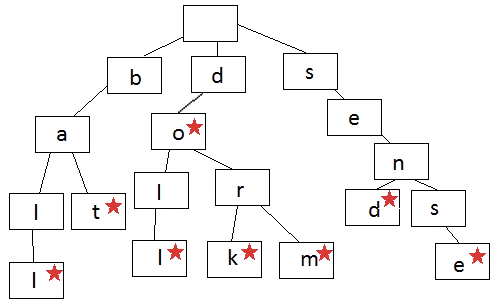
前缀树的一般结构如上图所示,有星号标记的表示从上到下到这个标记为止的字符序列构成一个单词,这个树中存储的词就有“ball”、“bat”、“doll”、“dork”、“dorm”、“send”、“sense” 这几个。
从这棵树的构造中,不难看出几点:
- 首先,根节点不存储字符,其余节点每个节点存储一个字符,同时存有指向子节点的指针。
- 其次,可以看到,我们做到了节点上的数据复用,极端一点,假设我们给定的大文件中所有的字符序列都是以字符‘a’ 开头的,本来我们可能需要存10亿个‘a’,现在只要存一个‘a’ 就可以了。此外,其检索速度也很快,假设你要查“abc” 是否在文件中出现过,构造完前缀树后,第一个词我们只需要顺着‘a’ 找下去,剩下的‘b’、‘c’、‘d’ ... 可能出现的25 条检索分支都给砍掉了,接下来找‘a’ 下面的‘b’分支,续行此法... ,因此其速度之快可见一斑,查找一个单词的速度就是O(一个单词的长度)。
当然了,树如其名,从上图可以看出,我们也可以查找一个词的前缀是否出现过,也就能实现Google 那种检索要求。
如何实现前缀树
先考虑如何构建,然后实现检索功能。
构建树的话,显然要看存储的数据的字符集,如果是ASCII 码,那就很简单,26 个英文字母就更简单了。不过考虑如果有中文、日文、韩文等等世界文体出现,我们就需要用Unicode 字符集了。
其次,节点包含的数据类型,可以考虑用一个指针数组来存储,数组里面放着指向下一层节点的指针。当然偷偷懒用一个hashmap 来实现之更方便。
这里,借用LeetCode 上一道题目来实现Trie Tree 和其基本的功能:
Implement Trie (Prefix Tree)
Implement a trie with insert, search, and startsWith methods.
Note: You may assume that all inputs are consist of lowercase letters a-z.
下面是我的Golang 代码:
type Trie struct {
next map[rune]*Trie
isWord bool
}
func Constructor() Trie {
return Trie{next: make(map[rune]*Trie), isWord: false}
}
func (t *Trie) Insert(word string) {
for _, v := range word {
if t.next[v] == nil {
t.next[v] = &Trie{next: make(map[rune]*Trie), isWord: false}
}
t = t.next[v]
}
t.isWord = true
}
func (t *Trie) Search(word string) bool {
node := t.prefixNode(word)
return node != nil && node.isWord
}
func (t *Trie) StartsWith(prefix string) bool {
node := t.prefixNode(prefix)
return node != nil
}
// prefixNode returns node related with prefix or nil if this node is not exist.
func (t *Trie) prefixNode(prefix string) *Trie {
for _, v := range prefix {
if t.next[v] == nil {
return nil
}
t = t.next[v]
}
return t
}
高级用法
更多的花式玩法是有的,稍微用点心 「做事情不用心的话,还做来干嘛呢,不如躺着睡觉,修心养性去~」 ,你会发现,在ACM 中,有很多问题需要结合多种数据结构来实现,一般以一主一辅/一主多辅的形式出现,这种做法主要是解决时空限制。因为ACM 竞赛中,对时间卡的尤其严,一般一个问题300MS 还解决不了,基本没戏了。
更现实一点就是,最近在做一个DNS 服务器的缓存模块,核心就是用前缀树实现的,不过加上垃圾回收,并发访问,递归遍历,进一步考虑如何对节点加锁/解锁、如何防止死锁出现,还是需要费不少劲。这也是本文的直接驱动力。
这里,拿LeetCode 上一道难度等级为Hard 的题目来展示下其妙用:
Word Search II
Given a 2D board and a list of words from the dictionary, find all words in the board.
Each word must be constructed from letters of sequentially adjacent cell, where "adjacent" cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
For example,
Given words = ["oath","pea","eat","rain"] and board =
[
['o','a','a','n'],
['e','t','a','e'],
['i','h','k','r'],
['i','f','l','v']
]
Return ["eat","oath"].
Note:
You may assume that all inputs are consist of lowercase letters a-z.
Hint:
You would need to optimize your backtracking to pass the larger test. Could you stop backtracking earlier?
If the current candidate does not exist in all words prefix, you could stop backtracking immediately. What kind of data structure could answer such query efficiently? Does a hash table work? Why or why not? How about a Trie?
下面是我用Golang AC 的代码,主要思想就是用前缀树实现剪枝辅助回溯深搜:
func findWords(board [][]byte, words []string) []string {
if len(board) == 0 || len(words) == 0 {
return nil
}
trie := constructor()
for _, word := range words {
trie.insert(word)
}
newBoard := pretreatBoard(board)
ss := NewSearchSet(trie, newBoard)
for i := 0; i < len(board); i++ {
for j := 0; j < len(board[0]); j++ {
ss.dfs(i+1, j+1)
}
}
return ss.result()
}
// generateVisit returns a 2'D array which flag a position whether was visited.
func generateVisit(len int) [][]bool {
visit := make([][]bool, len)
for i := range visit {
visit[i] = make([]bool, len)
}
return visit
}
// pretreatBoard returns a newBoard used 0 to surround board.
func pretreatBoard(board [][]byte) (newBoard [][]byte) {
row := len(board)
col := len(board[0])
newBoard = make([][]byte, row+2)
for i := range newBoard {
newBoard[i] = make([]byte, col+2)
}
for i := 0; i < len(board); i++ {
for j := 0; j < len(board[0]); j++ {
newBoard[i+1][j+1] = board[i][j]
}
}
return newBoard
}
type searchSet struct {
trie *trie // trie store all words which will be searched
board [][]byte // a board should surround with 0
visited [][]bool // visited flag whether current character was visited.
// resultWords is result words which can be found in board.
// Here use resultWords as a set, because maybe there has
// many path to find an identical word.
resultWords map[string]struct{}
dynamicArr [1 << 10]rune // dynamicArr record one path. Suppose a word length less than 1024.
index int // index record index of dynamicArr
}
func NewSearchSet(t *trie, board [][]byte) *searchSet {
return &searchSet{
trie: t,
board: board,
visited: generateVisit(len(board)),
resultWords: make(map[string]struct{}),
}
}
func (s *searchSet) dfs(row, col int) {
s.dynamicArr[s.index] = rune(s.board[row][col])
if !s.trie.startsWith(string(s.dynamicArr[:s.index+1])) {
return
}
if s.trie.search(string(s.dynamicArr[:s.index+1])) {
s.resultWords[string(s.dynamicArr[:s.index+1])] = struct{}{}
// NOTE: can not return, because maybe prefix in tree is a word
}
s.visited[row][col] = true
s.index++
if s.board[row+1][col] != 0 && !s.visited[row+1][col] {
s.dfs(row+1, col)
}
if s.board[row-1][col] != 0 && !s.visited[row-1][col] {
s.dfs(row-1, col)
}
if s.board[row][col+1] != 0 && !s.visited[row][col+1] {
s.dfs(row, col+1)
}
if s.board[row][col-1] != 0 && !s.visited[row][col-1] {
s.dfs(row, col-1)
}
s.index--
s.visited[row][col] = false
}
// result returns all words which can be found in board.
func (s *searchSet) result() []string {
var words []string
for word := range s.resultWords {
words = append(words, word)
}
return words
}
type trie struct {
next map[rune]*trie
isWord bool
}
func constructor() *trie {
return &trie{next: make(map[rune]*trie), isWord: false}
}
func (t *trie) insert(word string) {
for _, v := range word {
if t.next[v] == nil {
t.next[v] = &trie{next: make(map[rune]*trie), isWord: false}
}
t = t.next[v]
}
t.isWord = true
}
func (t *trie) search(word string) bool {
node := t.prefixNode(word)
return node != nil && node.isWord
}
func (t *trie) startsWith(prefix string) bool {
node := t.prefixNode(prefix)
return node != nil
}
// prefixNode returns node related with prefix or nil if this node is not exist.
func (t *trie) prefixNode(prefix string) *trie {
for _, v := range prefix {
if t.next[v] == nil {
return nil
}
t = t.next[v]
}
return t
}
既然扯到了深搜和剪枝,又翻开一两年前写的几篇博文看看,觉得还是有些参考价值,索性附上来:
回溯深搜与剪枝初步
OpenJudge_1321:棋盘问题
写到最后,想起来在顾森的书「思考的乐趣」中的序言里的一段对话:
学生:“咱家有的是钱,画图仪都买得起,为啥作图只能用直尺和圆规,有时还只让用其中的一个?”
老师:“上世纪有个中国将军观看学生篮球赛。比赛很激烈,将军却慷慨地说,娃们这么多人抢一个球?发给他们每人一个球开心地玩。”
数学文化微博评论:生活中更有意思的是战胜困难和挑战所赢得的快乐和满足。
All Rights Reserved.
Author:姜鹄.
Copyright © xp_jiang.
转载请标明出处:http://www.cnblogs.com/xpjiang/p/5399219.html
以上.