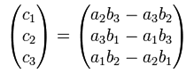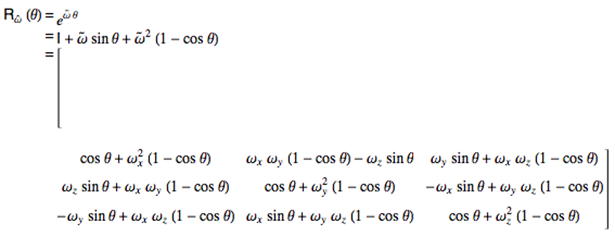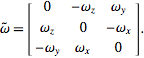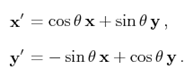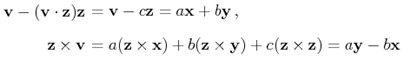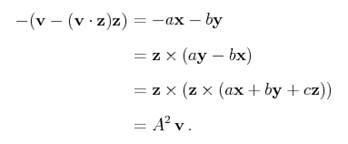根据旋转前后的向量值求旋转矩阵

如果已知旋转前后的一向量的变化，那么该如何求这个旋转矩阵呢？本篇结合Rodrigues' rotation formula，介绍一下该旋转矩阵的求法。

1.旋转角度

已知旋转前向量为P, 旋转后变为Q。由点积定义可知：

可推出P，Q之间的夹角为：

2. 旋转轴

由1中可知，旋转角所在的平面为有P和Q所构成的平面，那么旋转轴必垂直该平面。

假定旋转前向量为a(a1, a2, a3)， 旋转后向量为b（b1, b2, b3)。由叉乘定义得：

所以旋转轴c(c1, c2, c3)为：

3.  罗德里格旋转公式(Rodrigues' rotation formula)

3.1 公式

已知单位向量 ， 将它旋转θ角。由罗德里格旋转公式，可知对应的旋转矩阵 ：

其中I是3x3的单位矩阵，

是叉乘中的反对称矩阵r：

3.2 公式证明

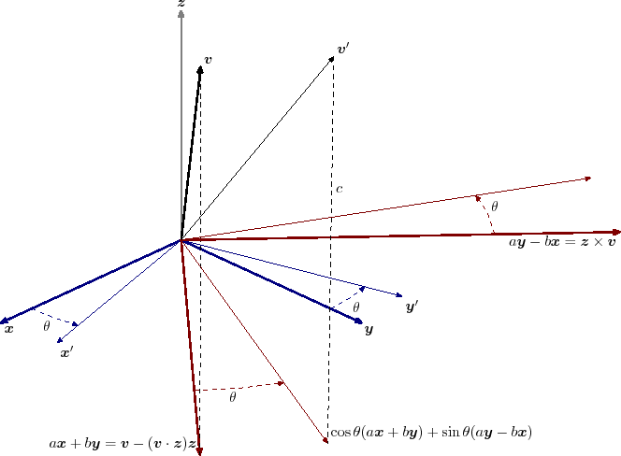
假设在坐标系(x, y, z）中，向量v=ax+by+cz，v绕z轴逆时针旋转θ角后得到新的向量v’。

根据2维（x,y)面上的旋转公式可得：

推出：

已知：

将上式带入v’的公式：

  将cz替换掉，可得：

将上式中的叉乘表示为反对称矩阵得：

另外：

最终可以推出：

上式即为罗德里格旋转公式。

4. 求旋转矩阵

根据旋转前后的两个向量值，使用上面的方法，先求出旋转角度和旋转轴，然后用罗德里格旋转公式即可求出对应的旋转矩阵。

C#的实现代码如下：

void Calculation(double[] vectorBefore, double[] vectorAfter)
{
    double[] rotationAxis;
    double rotationAngle;
    double[,] rotationMatrix;
    rotationAxis = CrossProduct(vectorBefore, vectorAfter);
    rotationAngle = Math.Acos(DotProduct(vectorBefore, vectorAfter) / Normalize(vectorBefore) / Normalize(vectorAfter));
    rotationMatrix = RotationMatrix(rotationAngle, rotationAxis);
}

double[] CrossProduct(double[] a, double[] b)
{
    double[] c = new double[3];

    c[0] = a[1] * b[2] - a[2] * b[1];
    c[1] = a[2] * b[0] - a[0] * b[2];
    c[2] = a[0] * b[1] - a[1] * b[0];

    return c;
}

double DotProduct(double[] a, double[] b)
{
    double result;
    result = a[0] * b[0] + a[1] * b[1] + a[2] * b[2];

    return result;
}

double Normalize(double[] v)
{
    double result;

    result = Math.Sqrt(v[0] * v[0] + v[1] * v[1] + v[2] * v[2]);

    return result;
}

double[,] RotationMatrix(double angle, double[] u)
{
    double norm = Normalize(u);
    double[,] rotatinMatrix = new double[3,3];
    
    u[0] = u[0] / norm;
    u[1] = u[1] / norm;
    u[2] = u[2] / norm;

    rotatinMatrix[0, 0] = Math.Cos(angle) + u[0] * u[0] * (1 - Math.Cos(angle));
    rotatinMatrix[0, 0] = u[0] * u[1] * (1 - Math.Cos(angle) - u[2] * Math.Sin(angle));
    rotatinMatrix[0, 0] = u[1] * Math.Sin(angle) + u[0] * u[2] * (1 - Math.Cos(angle));

    rotatinMatrix[0, 0] = u[2] * Math.Sin(angle) + u[0] * u[1] * (1 - Math.Cos(angle));
    rotatinMatrix[0, 0] = Math.Cos(angle) + u[1] * u[1] * (1 - Math.Cos(angle));
    rotatinMatrix[0, 0] = -u[0] * Math.Sin(angle) + u[1] * u[2] * (1 - Math.Cos(angle));
      
    rotatinMatrix[0, 0] = -u[1] * Math.Sin(angle) + u[0] * u[2] * (1 - Math.Cos(angle));
    rotatinMatrix[0, 0] = u[0] * Math.Sin(angle) + u[1] * u[2] * (1 - Math.Cos(angle));
    rotatinMatrix[0, 0] = Math.Cos(angle) + u[2] * u[2] * (1 - Math.Cos(angle));

    return rotatinMatrix;
}