《编译原理》-用例题理解-自底向上的语法分析,FIRSTVT,LASTVT集
上一篇:编译原理-用例题理解-自顶向下语法分析及 FIRST,FOLLOW,SELECT集,LL(1)文法
本笔记是对教材《编译原理》- 张晶老师版 做学习笔记。
本篇就是第 5 章的笔记。
(一)自底向上的语法分析概述
自底向上语法分析
自底向上语法分析从待输入的符号串开始,利用文法的产生式步步向上归约,试图归约到文法的开始符号。
从语法树的角度看
自底向上分析的过程是以输入符号串作为端末结点符号串,向着根结点的方向往上构造语法树,是开始符号正好是该语法树的根结点。
自底向上语法分析过程实际上是一个不断进行直接归约的过程
移进-规约大意:
用一个寄存符号的先进后出栈,把输入符号一个一个地移进到栈里,当栈顶符号串形成可归约串时(某个产生式的右部时),即把这个可归约串替换成(归约成)该产生式的左部的非终结符。
自底向上语法分析法基本思想
自左向右地扫描输入符号串,一遍把输入符号逐个移进分析栈,一边检查分析栈的栈顶符号串是否已经形成了句柄(句柄就是每个产生式的右部),如果形成句柄就把栈顶符号串替换为相应产生式左部的非终结符号,这种替换就称规约,再根据规约后的新栈顶,继续扫描,移进,规约。
例题:移进-规约
题目:
给定文法 G[S]:
(1)S -> aABe
(2)A -> b
(3)A -> Abc
(4)B -> d
解析:
步骤: 1 2 3 4 5 6 7 8 9 10
动作: 进 进 归 进 进 归 进 归 进 归
a b (2) b c (3) d (4) e (1)
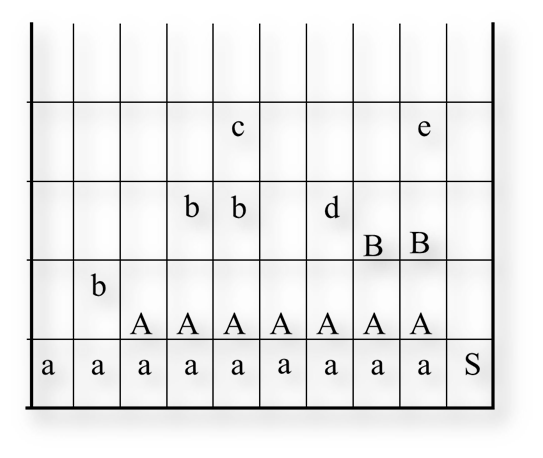
执行时,首先分析栈中会存放 # 到栈底,图上没有体现出来,应该在 a 的下面加上 #,将余留输入串最左边的字符放在分析栈栈首,此时栈中为 a,分析上面 4 句文法,文法的右部没有完全匹配的,所以没有构成句柄。
此时,继续移进第二个输入符号 b,此时栈顶的 b 与文法的(4)产生式的右部匹配,用 A -> b 规约,得到栈中为 aA
然后移进 b,c,用文法的(3)产生式进行规约。
直到最后 aABe,用产生式(1)规约出 S 开始符号,接受。
用表格表示:
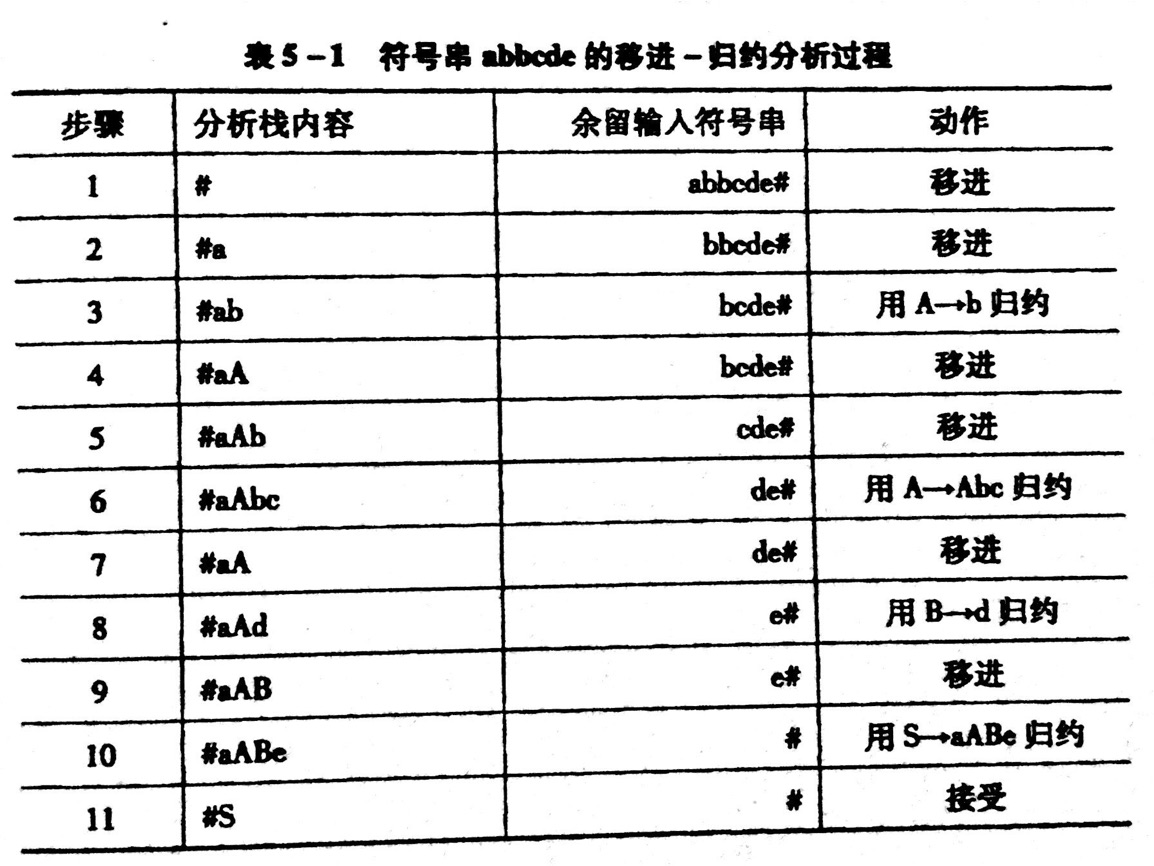
(图片来自教材:《编译原理》张晶老师版)
用树型表示:
每一次规约就相当于构造一颗子树,指导输入串结束时,构造成整个语法树。
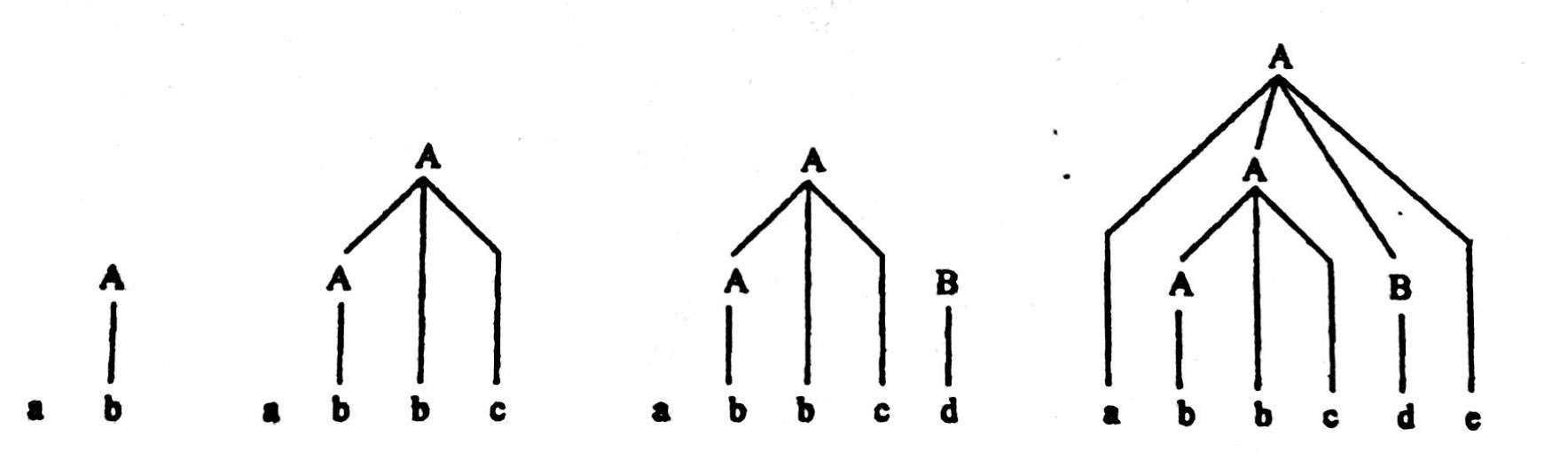
(图片来自教材:《编译原理》张晶老师版)
关于规范规约
首先,自底向上的分析的移进 - 规约过程是自顶向下最右推导的逆过程。
怎么理解呢?
最右推导是每次先推导最右边的非终结符,自顶向下的最右推导就是从开始符号开始,每次执行最右推导,推出输入符号串,最右推导是先推出输入串最右端的终结符,最后推出最左端的终结符。
那逆过程就是从输入符号串开始,每次先从最左端的终结符推导,最后推出开始符号。也就是自底向上的分析的移进 - 规约过程。
理解这句话之后,因为最右推导被称为规范推导,那么自左向右的规约则称为规范规约。
关于句柄
归约过程中,当句柄出现在栈顶符号串时,则用句柄归约。所以关键是在分析过程中如何确定句柄。
寻找句柄的方法不同,也就形成了不同的自底向上分析法。我们将介绍两种不同的方法,分别是优先分析法和 LR 分析法。
句柄就是每个产生式的右部。
句柄具有 “最左” 特征,这一点对于移进-归约过程很重要。
因为:句柄的 “最左” 性和符号栈的栈顶是相关的。对于规范句型来说,句柄的后面不会出现非终结符号(即,句柄的后面只能是终结符)。
基于这一点,我们可以用句柄来刻划 “可归约串”。因此,规范归约的实质是,在移进过程中,当发现栈顶呈现句柄时,就用相应产生式的左部符号进行替换。
优先分析法
优先分析法是在文法的一些符号之间建立所谓的优先关系,它又可以分为简单优先分析法 和 算符优先分析法
LR 分析法
根据分析过程中迄今已经取得的信息,并向前查看若干个输入符号来确定当前应采取的分析动作,及移进,规约,接受或报错。
可归约串
每实现异步规约都是把一串符号的用某个产生式的左部符号来代替,我们可以把栈顶上的这串符号成为 “可规约串”。事实上,存在种种不同的方法刻画 “可规约串”。
对这个概念的不同定义,也就形成了上述不同的自底向上的分析法。
- 优先分析法
- 简单优先分析法(句柄)
- 算符优先分析法(最左素短语)
即在 算符优先分析 中,我们用 “最左素短语” 来刻画 “可规约串”
- LR分析法(句柄)
(二)短语,直接短语,句柄
还有一个概念需要理解,句型,一起看。
句型的短语,直接短语定义:
若 S 是文法 G 的开始符号,αβδ 是该文法的一个 句型(能通过这个文法推导出来),即 S =*> αβδ,其中 α,δ ∈ V*,β ∈ V+。
如果有 S =*> αβδ 且 A=+>β,其中 A ∈ VN,则称 β 是句型 αβδ 相对于非终结符 A 的 短语。
另外,如果满足 S=*>αβδ,且 A -> β 是文法 G 的一个产生式,则称 β 是句型 αβδ 相对于非终结符 A 的 直接短语。
句型的句柄定义:
在一个句型中可以有多个直接短语,位于句型 最左边的直接短语 就称为 句柄。
例题:找短语,直接短语,句柄
题目:
给定文法:
(1)T -> T*F
(2)F -> F↑P|P
(3)P -> (T)|a
对于句型 T*P↑(T*F)
解析:
(1)根据 T =*> T*P↑(T) 和 T =*> T*F(即产生式1),可知 T*F 是该句型的 相对于 T 的 直接短语。
(2)根据 T =*> T*P↑P(由产生式1和2推出) 和 P =*> (T*F)(由产生式1和3推出),可知 (T*F) 是该句型的 相对于 F 的短语。
(3)根据 T =*> T*F↑(T*F) 和 F => P,可知 P 是该句型的 相对于 F 的 直接短语。
(4)根据 T =*> T*F 和 F =*> P↑(T*F),可知 P↑(T*F) 是该句型的 相对于 F 的短语。
(5)根据 T =*> T 和 T =*> T*P↑(T*F),可知 T*P↑(T*F) 是该句型的 相对于 T 的 短语。
综上,T*P↑(T*F) 共有 5 个短语,其中两个是直接短语,由于直接短语 P 是句型的最左直接短语,所以 P 是句型的 句柄。
通俗的说一下,上面 5 个短语的两个条件能推出该句型,可以看出来。那么条件又是怎么来的呢?怎么知道怎么划分短语呢?这个就是通过句型和文法中个各个产生式来推,但这样很不直观,也容易漏。
怎么更快的找出所有短语,直接短语和句柄呢?
找出所有短语,直接短语和句柄,一种方法是根据定义寻找,显然,这种方法不直观,而且很难知道是否已穷尽所有情况;
另一种方法是利用语法树,首先为给定句型构造一颗语法树然后利用这棵语法树就可以找出该句型全部的短语,直接短语和句柄。
还对上题分析,使用语法树分析:
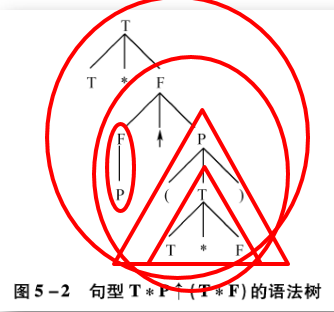
(图片来自教材:《编译原理》张晶老师版)
从底向上看,找子树
(1)T -> T*F
(2)P -> (T*F)
(3)F -> P
(4)F -> P↑(T*F)
(5)T -> T*P↑(T*F)
再根据文法中的产生式判断:
- 直接短语(文法中包含产生式),有子树(1),子树(3),就是说他俩为直接短语
- 句柄(最左直接短语),比较(1)和(3)谁在左边
对语法树的剪枝方法
(1)每个句型都有一个语法树
(2)每个语法树(整棵树)的端末结点自左向右排列就组成一个 句型
(3)每棵 子树的端末结点 自左向右排列就组成一个 短语
(4)每棵 简单子树的端末结点 自左向右排列就组成一个 直接短语
(5)最左简单子树的端末结点自左向右排列就组成一个 句柄
(三)简单优先分析法
优先分析法分为:
- 简单优先分析法(句柄)
- 算符优先分析法(最左素短语)
简单优先分析法是一种典型的 自底向上 的分析法,它符号串进行语法分析的过程是一个 规范规约 的过程。
它首先对文法 按一定规则 求出 所有符号(即终结符和非终结符) 之间的 优先关系,然后在分析过程中根据文法符号之间的 简单优先关系 来寻找符号串中可以进行规约的子串(即句柄)来进行规约。
简单优先文法
由于简单优先分析法是按照文法符号之间的 优先关系 来确定句柄的,所以首先要介绍两个文法符号之间存在的优先关系,然后介绍优先关系是 怎样确定的 和 如何构造关系表。
三种简单优先关系:
在简答优先文法中,两个文法符号之间可以是下述三种优先关系之一:

注意:
上面所引入的是三种优先关系都是对文法中的符号序偶来定义的,这三种关系和数学中的 =,<,> 不同,它们是有序的,就是不满足交换律,即
Si <· Sj 不一定有 Sj <· Si
详细:
(1)第一种关系 - Si 和 Sj 优先级相同
(2)第二种关系 - Si 的优先级低于 Sj
(3)第三种关系 - Si 的优先级高于 Sj
(4)第四种关系 - 不存在优先关系。这个上面没有体现。
例题:已知文法,求优先关系
题目:
给定文法:
(1)S -> (R)|A|∧
(2)R -> T
(3)T -> S,T|S
注意:(3)中的逗号是终结符
求文法符号之间的优先关系:
解析:
为了更好理解,直接上截图,注意逗号的理解,并列逗号和终结符中的逗号。

简单优先文法定义:
简单文法是满足以下条件的文法:
(1)在文法字汇表中,任意两个符号之间至多存在一种简单优先关系
(2)文法中的任意两个产生式没有相同的右部(唯一性)
简单优先关系矩阵
对上面例题,做出简单优先关系矩阵
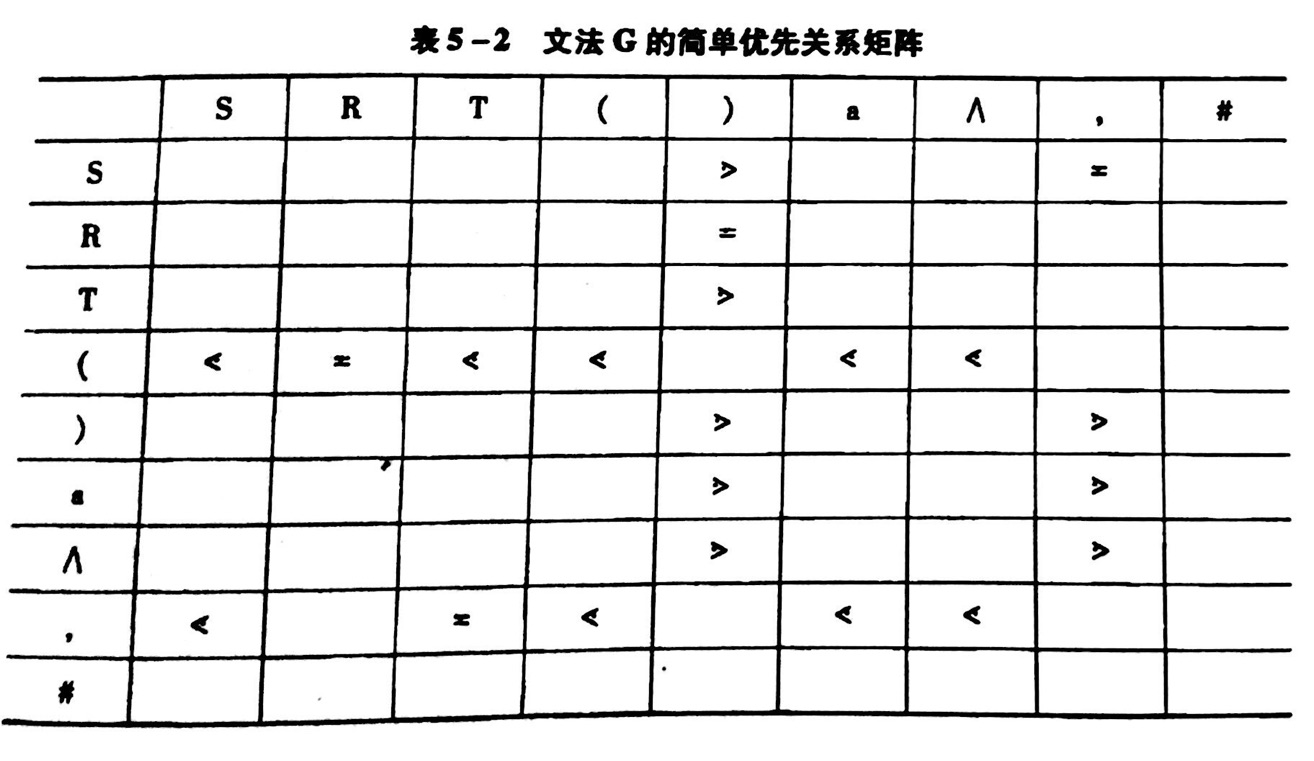
(图片来自教材:《编译原理》张晶老师版)
简单优先分析法定义:
对简单优先文法的分析方法就是简单优先分析法。
简单优先分析法的局限性:
简单优先分析法只适应于简单优先文法。实际上,一般的程序设计语言的文法都不是简单优先文法。
所以,虽然简单优先分析法准确、规范,但分析效率较低,而且实际使用价值不大,更多可以看书,此处不再描述
(四)算符优先分析法
算符优先分析法是一种古典又实用的方法。
算符优先文法(OPG文法)定义
简单优先分析法 规定了文法符号间 (非终结符 VN 和终结符 VT) 的优先顺序和结合性质,然后借助这种优先关系和结合顺序来寻找可归约串(句柄)进行归约。
算符优先分析法 规定了算符间 (终结符 VT) 的优先顺序和结合性质,然后借助这种优先关系和结合顺序来寻找可归约串(最左素短语)进行归约。
通俗的说,算符优先分析法借助于终结符之间的优先关系确定可归约串。由于它不考虑非终结符之间的优先级关系,而且在规约过程中只要找到句柄就规约,并不考虑规约到哪个非终结符,因而算符优先规约并不是规范规约,确切的说,可规约串是最左素短语,而不是句柄。
特别有利于表达式分析,宜于手工实现。
但是它能力不强,仅能对算符优先文法进行分析。
算符优先分析法的分析过程是一种自下而上的归约过程,但这种归约未必是严格的最左归约。即 算符优先分析法不是一种规范归约法。
使用工具: 优先表、总控程序、栈
定义算符优先分析法前,先定义算法文法。
算符文法定义
若在上下文无关文法 G 中,不含 ε-产生式,且不含形如 U → …AB…的产生式,则称 G 为算符文法,也称 OG 文法 (Operater Grammar)
算符文法要满足:
- 不含ε-产生式;
- 产生式右部不包含两个相邻非终结符
算符优先分析法中,要利用 终结符 之间的 优先关系 来找出句柄,所以要先给出终结符之间存在的三种优先关系。

(图片来自教材:《编译原理》张晶老师版)
用语法树表示:
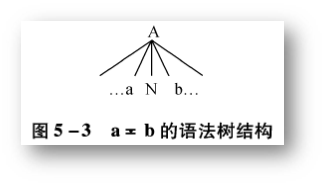
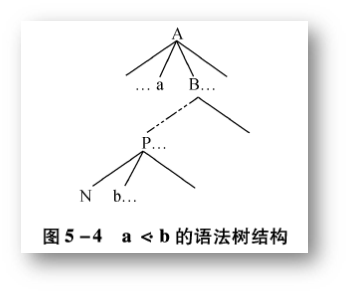
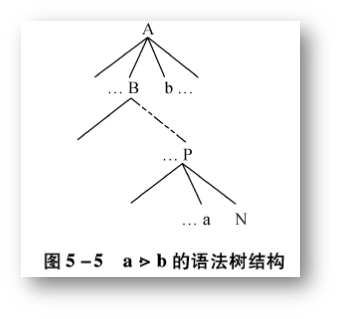
例题:判断 G 是否是 OPG 文法
题目:
对于文法 G(E):
(1)E -> E+T|T
(2)T -> T*F|F
(3)F -> (E)|i
(1)判断 G 是否是 OG 文法(算符文法);
(2)再找出 G 中所有终结符对的优先关系;
(3)最后判断 G 是否是 OPG 文法(算符优先文法)
解析:
(1)判断 G 是否是 OG 文法(算符文法),根据算符文法要满足:
- 不含ε-产生式;
- 产生式右部不包含两个相邻非终结符
(2)再找出 G 中所有终结符对的优先关系,得出优先关系表
具体怎么构造关系表,在下面有提
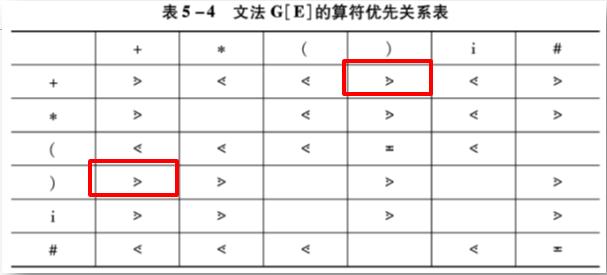
(图片来自教材:《编译原理》张晶老师版)
(3)最后判断 G 是否是 OPG 文法(算符优先文法)
由于对于 G(E) 的任何终结符对(a,b)至多只有一种优先关系成立,即优先关系表中不存在多重入口,所以,文法 G(E) 是一个算符优先文法

优先关系表的构造
由定义构造缺乏可操作性。所以选择由算法构造。
为了找出所有优先关系,使得优先关系表没有疏漏,要对 G 的每个非终结符 T 构造两个集合:FIRSTVT集(最左终结符集),LASTVT集(最右终结符集)
FIRSTVT 集,LASTVT 集定义:

FIRSTVT(T) 的构造规则(必背)
(1)若有 T→a… 或 T→Ra…,则 a∈FIRSTVT(T);
(2)若 a∈FIRSTVT(R),且有产生式 T→R…,则 a∈FIRSTVT(T)
LASTVT(T) 的构造规则(必背)
(1)若有 T→…a 或 T→…aR,则 a∈LASTVT(T);
(2)若 a∈LASTVT(R),且有产生式 T→…R,则 a∈LASTVT(T)
例题:求 FIRSTVT,LASTVT 集
题目:
对于文法 G(E):
(1)E -> E+T|T
(2)T -> T*F|F
(3)F -> (E)|i
结果:
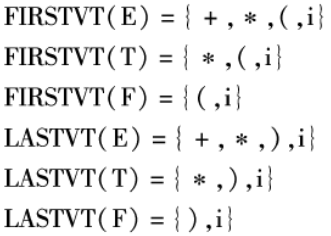
具体说一下怎么来的,
第一个 FIRSTVT(E) 集
- 由文法(1)和规则(1)得出 + ∈ FIRSTVT(E)
- 由文法(2)和规则(1)得出 * ∈ FIRSTVT(T)
- 由文法(1)和规则(2)得出 * ∈ FIRSTVT(E)
- 由文法(3)和规则(1)得出 ( ∈ FIRSTVT(F)
- 由文法(2)和规则(2)得出 ( ∈ FIRSTVT(T)
- 由文法(1)和规则(2)得出 ( ∈ FIRSTVT(E)
- 由文法(3)和规则(1)得出 i ∈ FIRSTVT(F)
- 由文法(2)和规则(2)得出 i ∈ FIRSTVT(T)
- 由文法(1)和规则(2)得出 i ∈ FIRSTVT(E)i
上面为了容易理解,分开写,但不直观,同理也可以根据 LASTVT 集规则计算出 LASTVT 集。
素短语
在这里插入图片描述 素短语是满足下面条件的短语:
- 至少包含一个终结符。
- 该短语不再包含满足第一个条件的更小的短语。
最左素短语:
处于句型最左边的那个素短语
算符优先分析算法就是根据 最左素短语 的定理构造的
算符优先分析算法的实现
工作原理: 对当前句型不断寻找最左素短语进行归约的过程。寻找最左素短语时,首先找到最左素短语的末尾终结符,然后再向前搜索最左素短语的首终结符。
使用的数据结构: 栈,数组。
有关约定:#作为语句括号,视为终结符,其优先级最低。
算符优先分析的局限性
算符优先分析 比规范归约要快得多,因为它跳过了所有单个非终结符的归约。
忽略非终结符的归约 在归约过程中存在某种 危险性,可能导致把本来不是文法句子的输入串误认为是文法的句子,即会把错误的句子得到正确的归约。
总结
算符优先分析算法与简单优先分析算法的比较
两个算法类似,所不同的是 算符优先分析算法 每一步归约 不一定是规范归约,而是找出最左素短语进行归约,并且在寻找最左素短语的过程中,只比较终结符之间优先关系,不受非终结符的影响
比较表格:
| - | 简单优先分析法 | 算符优先分析法 |
|---|---|---|
| 语法分析类别 | 自上而下分析 | 自下而上分析 |
| 可规约串 | 句柄 | 最左素短语 |
| 确定可规约串的根据 | 任意两文法符号之间的简单优先关系 | 任意两终结符之间的算符优先关系 |
| 效率比较 | 效率较低 | 只考虑终结符,效率较高 |