题意
给定(N,A,B),求长度为(n)的排列(P)数量,满足最长上升子序列长度不超过(2),且(P_A=B)。
题解
首先可以令(P'_i=N-P_i+1),同时将题面里LIS不超过(2)变成LDS不超过(2)。
首先,如果(A>B),我们可以交换排列的下标和值(即原来(P_i=j),现在(P'_j=i)),那么原来的LIS依然是LIS,而LDS依旧是LDS。
为什么呢?因为如果原来有(i_1<i_2<i_3dots<i_k)以及(P_{i_1}<P_{i_2}<P_{i_3}dots P_{i_k}),那么你交换下标和值以后这些条件依然满足。LDS同理。
因此现在就只需要考虑(Ale B)的情况了。
我们将序列(P)中是前缀最大值的位置拿出来,我们发现那些不是前缀最大值的元素一定是递增的,因为任何一个不是前缀最大值的元素都可以和它前面一个前缀最大值组成长度为(2)的下降子序列,所以如果它后面还有比他小的数的话,那么就组成了长度为(3)的下降子序列。
这也就意味着如果你确定了哪些位置是前缀最大值以及他们的值,我们就可以唯一对应一个满足条件的排列。因此我们只需要计数前者就行了。
但是我们还有(P_A=B)这个条件。我们发现因为(Ale B),所以这个数一定作为点缀最大值出现。
如果它不是前缀最大值,那他后面所有数都要比他大,而且它前面也至少要有一个比他大的,而后面有(n-A)个位置,即至少要有(n-A+1)个比他大的,但是比它大的数只有(n-B)个。由于(Ale B)所以(n-A+1>n-B),矛盾。
另外,如果前缀最大值序列(MX_i<i),这显然是不合法的。否则可以证明这是一个合法的(MX)序列。
那么我们的前缀最大值数组(MX_i)应该满足一下条件:
-
(MX_ile MX_{i+1})
-
(MX_N=n)
-
(MX_{A-1} e B,MX_{A}=B)
-
(MX_ige i)
我们把(MX)化成柱状图放在平面直角坐标系上,比如下图是一个(P={2,3,5,1,7,8,4,6},MX={2,3,5,5,7,8,8,8})的柱状图:
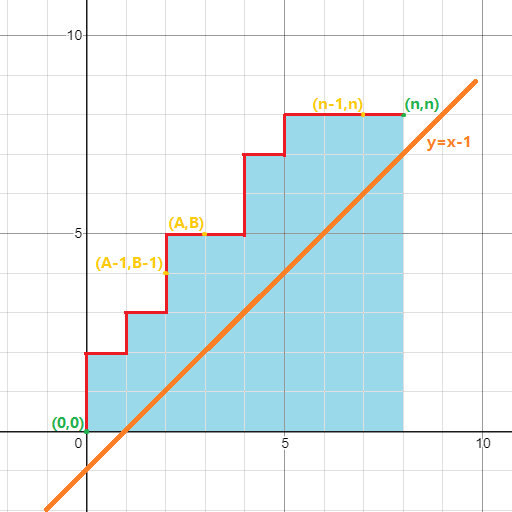
我们发现个柱状图轮廓的一部分(红色)是一个从((0,0))到((n,n))的,只能向右上移动的路径。
考虑我们对这条路径的限制。
首先,由于我们要求(MX_ige i),所以该路径不能与直线(y=x-1)(图中橙色)有交点。
由于(MX_n=n),因此路径中要存在((n-1,n)->(n,n))的部分。
由于(MX_A=B),所以路径中要存在((A-1,B)->(A,B))的部分,另外由于(MX_{A-1} e B)所以路径中要存在((A-1,B-1)->(A-1,B))的部分。(图中描述了(A=3,B=5)的情况)
综合上述条件,设(F(S_x,S_y,T_x,T_y))表示从((S_x,S_y))走到((T_x,T_y)),不接触直线(y=x-1)的方案数,那么答案为
(F(0,0,A-1,B-1) imes F(A,B,n-1,n))
至于(F)怎么求,是一个经典问题,它是从((S_x,S_y))走到((T_x,T_y))的方案数减去从((S_x,S_y))走到((T_x,T_y))关于直线(y=x-1)的对称点的方案数。
code:
#include<bits/stdc++.h>
#define ci const int&
#define C(x,y) (1ll*fac[x]*POW(fac[y],mod-2)%mod*POW(fac[x-(y)],mod-2)%mod)
using namespace std;
const int mod=1e9+7;
int n,a,b,fac[2000010];
int POW(int x,int y){
int ret=1;
while(y)y&1?ret=1ll*ret*x%mod:0,x=1ll*x*x%mod,y>>=1;
return ret;
}
int Calc(ci xs,ci ys,ci xe,ci ye){
return(C(xe-xs+ye-ys,xe-xs)-C(xe-xs+ye-ys,ye+1-xs)+mod)%mod;
}
int main(){
scanf("%d%d%d",&n,&a,&b),++a,++b,b=n-b+1,fac[0]=1;
for(int i=1;i<=(n<<1);++i)fac[i]=1ll*fac[i-1]*i%mod;
if(b<a)swap(a,b);
printf("%lld",1ll*Calc(0,0,a-1,b-1)*Calc(a,b,n,n)%mod);
return 0;
}