Python3实现最小堆建堆算法

今天看Python CookBook中关于“求list中最大(最小)的N个元素”的内容，介绍了直接使用python的heapq模块的nlargest和nsmallest函数的解决方式，记得学习数据结构的时候有个堆排序算法，所以顺便研究了一下“堆”结构（这里特指二叉堆）。

概念

所谓二叉堆（binary heap）实际上就是一颗特殊的完全二叉树，其特殊性在于：

1. 二叉树中所有的父节点的值都不大于/不小于其子节点；
2. 根节点的值必定是所有节点中最小/最大的。

父节点值不大于子节点且根节点值最小称为最小堆，反之称为最大堆。最大堆和最小堆没有本质上的区别。如下图是一个典型的最小堆：

 

算法

现在实现一个对给定list完成初始建堆的算法。（以最小堆为例）

假设 list = [1, 8, 2, 23, 7, -4, 18, 23, 42, 37, 2]

先记录一个自己当时看堆结构时琢磨出来的算法，后来查了查资料发现不是最优的。

渣渣算法

直接根据list中元素的index构建二叉树，这里我们不使用链表，完全以列表实现并以0为基（根节点index为0）：

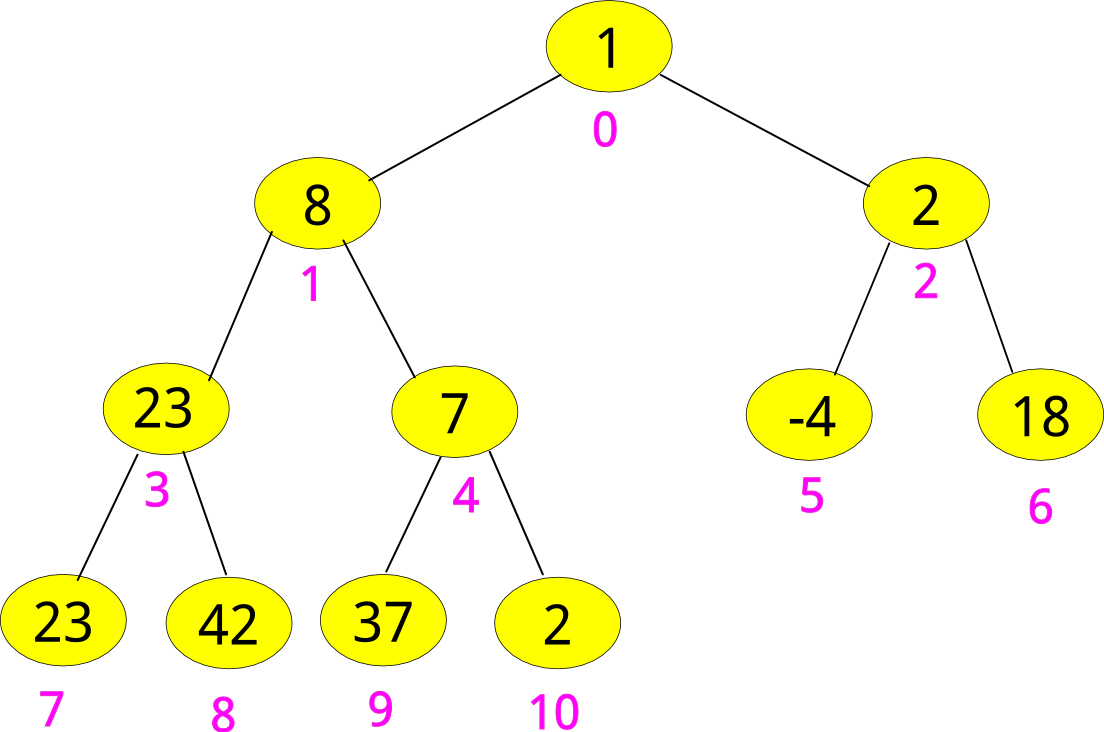
根据完全二叉树的特点（节点如果存在右子节点，则必存在左子节点且如果右子节点存在子节点，则左子节点必存在左右子节点），元素个数为N的完全二叉树的最后一个拥有子节点的节点的index为N//2 -1 。

为了实现二叉树中所有父节点的值不大于其子节点（特性1），只需要从根节点（index = 0）遍历到最后一个拥有子节点的节点（index = N//2 -1），将父节点与其子节点值作比较，必要时进行交换即可。完成一次上述过程后就能完成最底层节点的归位了。元素个数为N的二叉树层数为ceil(log₂n),因此一共执行floor(log₂n)次上述过程就能实现最小堆的建堆了。算法如下：

#!/usr/bin/env python

import os
import sys
import math

def heap(list):
    n = len(list)
    for i in range(0,int(math.log(n,2))):                #每循环依次就完成了一层的建堆
        for j in range(0,n//2):
            k = 2*j+2 if 2*j+2 < n and list[2*j+2] < list[2*j+1] else 2*j+1    #让k成为较小的子节点的index
            if list[j] > list[k]:
                (list[j],list[k]) = (list[k],list[j])         #交换值

def main(argv):
    list = [int(arg) for arg in argv]
    heap(list)
    print(list)
if __name__ == "__main__":
    if len(sys.argv) > 1:
        main(sys.argv[1:])

这是自顶向下的遍历方式，还可以自底向上遍历，则首先归位的是根节点。

很明显，这个算法的复杂度为O(nlogn), 但实际上，最优的建堆算法的复杂度是O(n)，而且这个算法还使用了数学函数。。。

最优算法

下面贴一个使用递归的最优算法：

思路还是一样，直接根据list构建二叉树，然后从最后一个拥有子节点的节点向上遍历，使用下沉算法将遍历到的每一个子树变成二叉堆。最终整个二叉树就成为一个二叉堆。

#!/usr/bin/env python

import os
import sys

def sink(list,root):
    if 2*root+1 < len(list):
        k = 2*root+2 if 2*root+2 < len(list) and list[2*root+2] < list[2*root+1] else 2*root+1     #让k成为较小的子节点的index
        if list[root] > list[k]:
            (list[root],list[k]) = (list[k],list[root])     #交换值
            sink(list,k)              #对子节点为根节点的子树建堆

def main(argv):
    list = [int(arg) for arg in argv]
    for i in range(len(list)//2-1,-1,-1):
        sink(list,i)
    print(list)
if __name__ == "__main__":
    if len(sys.argv) > 1:
        main(sys.argv[1:])

两种算法运行截图：

堆排序

最后说一下堆排序，建堆完成后，排序就简单了：

将根节点（即list[0]）弹出：list.pop(0)，然后将最后一个节点放到根节点位置，对剩下的list再次进行建堆（针对算法1，算法2则是直接调用sink方法即可）。反复此过程就能输出排序结果。

想要直接在list内排序的话，则不弹出根节点，而是直接将根节点和最后一个节点交换位置，反复调用sink方法（但是不能再用len(list)，而是给定一个从len(list)依次递减的参数，避免让已排序好的节点继续参与建堆）