A - 军队
问题描述
给定一个有 (n) 个队伍的人组成的序列,第 (i) 个队伍 (i) 有 (s[i])个人组成,一个 (l) 到 (r)的子序列是合法的,当且仅当(((∀i)(∀j)∧(i≠j)∧(l≤i,j≤r))→(gcd(s[i],s[j])=1)),即对于该序列中任两个不相同的队伍,他们人数的最大公约数为 (1),并且要求该子序列的总人数大于等于 (k)。
且由于每个队伍能够审批携带的仪器是有限的,所以需要这个队伍((r - l + 1))尽可能长,请求出这个队伍的最长长度,若不存在,请输出 (0)。
输入
第一行两个整数 (n,k) 分别表示队伍数量和人数下限
接下来一行 (n) 个整数,表示每个队伍的人数
输出
一行一个整数,表示队伍的最长长度,如果不存在一个这样的队伍,则输出 (0)
输入输出样例
样例输入
5 14
4 5 12 3 2
样例输出
2
数据范围
对于 (10\%)的数据 (n≤10)
对于另外 (20\%)的数据 (n≤100)
对于另外 (20\%)的数据 (n≤2 imes 1000)
对于全部的数据 (1≤n≤10^5, 1≤s[i]≤10^6, k≤ int)。
题解
枚举左端点及右端点即可,还要加一些玄学优化。
(n)方过十万!
代码
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cctype>
#define int long long
#define gI gi
#define itn int
#define File(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout)
using namespace std;
inline int gi()
{
int f = 1, x = 0; char c = getchar();
while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}
while (c >= '0' && c <= '9') {x = x * 10 + c - '0'; c = getchar();}
return f * x;
}
int n, k, a[100003], dp[100003], sum[100003];
namespace sub1
{
int gcd(int a, int b)
{
if (b == 0) return a;
return gcd(b, a % b);
}
bool pd(int l, int r)
{
for (int i = l; i <= r; i+=1)
{
for (int j = i + 1; j <= r; j+=1)
{
if (a[i] % 2 == 0 && a[j] % 2 == 0) return false;
if (gcd(a[i], a[j]) != 1) return false;
}
}
return true;
}
void getans()
{
itn ans = 0;
for (int i = 1; i <= n; i+=1)
{
for (int j = i + 1; j <= n; j+=1)
{
if (sum[j] - sum[i - 1] < k) continue;
if (pd(i, j)) ans = max(ans, j - i + 1);
}
}
printf("%lld
", ans);
return;
}
}
namespace sub2
{
int gcd(int a, int b)
{
if (b == 0) return a;
return gcd(b, a % b);
}
void getans()
{
int ans = 0;
for (int i = 1; i <= n; i+=1)
{
int Right;
for (Right = i; Right <= n; Right+=1) if (sum[Right] - sum[i] >= k) break;
bool fl = false;
for (int j = i; j <= Right && !fl; j+=1)
{
for (int k = j + 1; k <= Right && !fl; k+=1)
{
if (gcd(a[j], a[k]) != 1) fl = true;
}
}
if (fl) continue;
ans = max(ans, Right - i + 1);
for (++Right; Right <= n; Right+=1)
{
bool fl = false;
for (int j = i; j < Right && !fl; j+=1) if (gcd(a[j], a[Right]) != 1) fl = true;
if (fl) break;
ans = max(ans, Right - i + 1);
}
}
printf("%lld
", ans);
}
}
signed main()
{
File("tarmy");
n = gi(), k = gi();
for (int i = 1; i <= n; i+=1) a[i] = gi(), sum[i] = sum[i - 1] + a[i];
if (sum[n] < k) {puts("0"); return 0;}
if (n <= 100) {sub1::getans(); return 0;}
else {sub2::getans(); return 0;}
return 0;
}
B - 取石块儿
问题描述
小 (L) 和小 $T $进行取石块儿游戏,给定一个整数 (n) 表示石块儿总数,给定一个整数 (k) 表
示每次最多能拿走的石块儿数量,小 (L) 先手,每次能拿走 (1)~(k) 个石块儿,他们中总会有一
个人最后拿走 (s) 块儿石块儿,使得剩余石块儿数量为 (0),则最后一个拿走剩下石块儿的人获
胜,另外一个人失败。
小 (T) 非常聪明,小 (L) 绝顶(秃子(逃))聪明,请判断小 (T) 是否能取胜。
输入
第一行一个整数 (T) 表示数据组数,接下来 (T) 行每行两个整数 (n),(k) 意义为描述所给。
输出
对于每组数据,输出"(YES)"或者"(NO)"(不带引号),代表小 (T) 是否能够获胜。
输入输出样例
样例输入
2
2 1
10 4
样例输出
YES
YES
数据范围
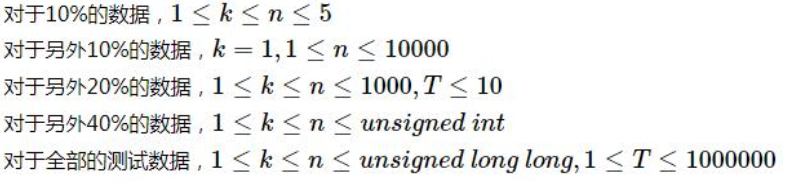
题解
首先对于只有(k)个石块儿的情况, 很明显直接一次拿走就能获胜, 对于有(k + 1)块石块儿情况, 不论怎么拿, 总会产生少于(k)块石块儿的情况, 于是是必败的。
同样, 对于((k + 1, k + k + 1])个石块儿的情况, 总能拿走一部分石块儿是的对手处于(k + 1)的必败情况, 归纳证明当(n \% (k + 1) == 0)的时候, 先手必胜, 反之后手必胜。
代码超短的……
代码
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cctype>
#define int unsigned long long
#define gI gi
#define itn int
#define File(x) freopen(x".in","r",stdin);freopen(x".out","w",stdout)
using namespace std;
inline int gi()
{
int f = 1, x = 0; char c = getchar();
while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}
while (c >= '0' && c <= '9') {x = x * 10 + c - '0'; c = getchar();}
return f * x;
}
int t, n, k, a, b;
signed main()
{
File("tstones");
t = gi();
while (t--)
{
n = gi(), k = gi();
if (k == 1)
{
if (n & 1) puts("NO");
else puts("YES");
}
else
{
if (n % (k + 1)) puts("NO");
else puts("YES");
}
}
return 0;
}
总结
这次练习做得不是很好。
要拿的很多部分分都没有拿到。
还要继续努力啊(QwQ)。