今天又是瞌睡的一天。（似乎每天打瞌睡应景成为常态，这样下去我不会猝死吧）
考试 8点写完t1的暴力25，想好50,9点写完t2 50分，一想都50分了，没有其他暴力了，干脆不搞正解什么的吧，10点发现t3只会20分，30的都不会，还以为又是什么转化转化变成数据结构，写了t1的剩下25分，t1的50有了，现在有120分了，应该是大家都有的分，于是想t3还有10分，看起来可做，结果又是个n^2 递推，不是组合数，卡特兰，和之前的斯特林数，自闭了，看看t1，整数分块套不上去啊，呜呜呜，看看t2，我只能暴力去搞，呜呜呜，乍一看还以为是群论，非常兴奋，终于能用到当初学了，从未用过的b***,p****,然后仔细一看，想了一个稍微好的暴力，打表发现1e5可过，1e6的话1.6e8差不多（打完表此时11点过一点），赶紧写了写交上去，最后还是50分，看了看，数据是捆绑的，呜呜呜，疑惑jyht180怎么来的，问老师t1最后50不是也是捆绑的吗，会道问jyh去，于是我灵光一现，看了看t1题面，偶，还有n<=50000的暴力。
总分:50+50+20.
今天发挥的还可以呀。
总结：t3的30没有想到很可惜呀，不过有更好的暴力还是要交的呀。
t1:
我是菜鸡
其实很简单。
把d固定，考虑不同的w。
在dfs过程中，用树状数组维护从1到x的路径上对于i的贡献.
t2:
实际上一眼就可以看出与置换有关。
求出环，求出ss,tt的最小循环节，不一样直接-1，让ss,tt的最小循环节去找ss最少需要几步到tt，这个过程用最小表示法完成，在求出最小步数p后，顺便check一下是否真的ss走p步就能到tt。不能-1.
然后我们就得到了很多组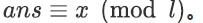
（l是最小循环节的长度）。
扩展中国剩余定理即可。
t3:
没有想到，呜呜呜。
重点是想到一开始的时候把a排序。（不然就困到数据结构里出不来了）
#include<bits/stdc++.h> using namespace std; const int N=3e5+5,mod=998244353; typedef long long ll; ll a[N],x; int n; int f[N]; int sum[N*60],ch[N*60][2],idx; int get(int p,int u,ll v)//注意求值时 a[i] 与 x 的0/1取值关系对答案取0取1的影响 { if(u<0||!p) return sum[p]; if(x>>u&1) return get(ch[p][1-(v>>u&1)],u-1,v); if(v>>u&1) return (sum[ch[p][0]]+get(ch[p][1],u-1,v))%mod; return (sum[ch[p][1]]+get(ch[p][0],u-1,v))%mod; } void insert(int &p,int u,ll v,int fv) { if(!p) p=++idx; sum[p]=(sum[p]+fv)%mod; if(u<0) return; if(v>>u&1) insert(ch[p][1],u-1,v,fv); else insert(ch[p][0],u-1,v,fv); } int main() { // freopen("xor.in","r",stdin); // freopen("xor.out","w",stdout); cin>>n; cin>>x; for(int i=1;i<=n;i++) scanf("%lld",&a[i]); sort(a+1,a+n+1); int rt=0; for(int i=1;i<=n;i++) { f[i]=(1+get(rt,60,a[i]))%mod; insert(rt,60,a[i],f[i]); } int ans=0; for(int i=1;i<=n;i++) ans=(ans+f[i])%mod; printf("%d",ans); return 0; }