(一)高阶差分方程的解:
高阶差分齐次方程:
1仍然可得 是该齐次方程的解
是该齐次方程的解
2得到对应的特征方程(其实以后我们可以直接写出相应的特征方程,参考高数中写微分方程的特征方程)

将有n个特征根(相异实数根,多重根,共轭复根)
(1)相异实根:

(2)实根,m重根:

这里只是举一个例子,太复杂的并没有阐述,即:阿尔法1到阿尔法m都相等吗,但阿尔法m+1到阿尔法n都是相异实根。(其实还是不够一般化)(注意,最后那个因为相等所以阿尔法1改写为了阿尔法m)(而且他没把剩下的相异实根 部分写上去,容易引起误解)
所以上面这个表述是有歧义的。因为假如重根有5个,分别为阿尔法1,2,3,4,5。但是他们的重数可能是不同的,比如重数分别为2,2,3,4,5.所以他们的上面这个表述是有问题的。
应该改为:

这里的n替换为t,这里仅是假设阿尔法1为k重,而其余的k+1到N个根都是相异实根。
那么其余的怎么写,就了然了。
看两个例子:


(3)复根

复根出现重根的情况不再给出了
(二)稳定性条件

要得到上述结论,需要先证明下式:

然后再由此式即可推导出上述结论。
(详细版笔记中我已证明和推导)
(三)非齐次特解
非齐次差分方程的形式和推动过程x(t)有关
即推动过程为确定性过程
下面几种为讨论推动过程包含常数项,时间趋势项t的情形。
(1) (高阶差分方程)
(高阶差分方程)
此时的方程为:
则猜想解的形式为:
代入方程,解出c的值为:
但是分母 可能为0,那么c就不存在了。
可能为0,那么c就不存在了。
此时,我们应猜想解的形式为:
代入方程,解出c的值为:
若分母 可能为0,那么c就不存在了。
可能为0,那么c就不存在了。
继续尝试 这样形式的解,知道找到为止,总能找到的。
这样形式的解,知道找到为止,总能找到的。
(2) 其中b,d,r都是常数(仅指出了一阶)
其中b,d,r都是常数(仅指出了一阶)
此时的方程为:
我们仅考虑一阶:
猜想解的形式为:
代入方程,接触c0,c1
于是,得到一个特解为:

只要|d^r|<1,该解就收敛
即:1
(常数项乘以了t)
2 ,尝试使用
,尝试使用
每一项都乘以了t
对于高阶方程,仍然可以使用此方法(不过猜想的第一个解需要一定的智慧)
(3) 其中b为常数,d为正常数。
其中b为常数,d为正常数。
此时的方程为:
猜想其特解的一般形式为:
举一个二阶差分方程的例子:
方程形式为: (此时d=1)
(此时d=1)
猜想其特解的一般形式为:
代入可能到两个系数为:

同样考虑 ,则令此时的特解形式为:
,则令此时的特解形式为:
(四)待定系数法
(待定系数法在微分方程中也常用,先猜一个挑战解,假定其满足,然后代入,最终去求出这些系数,如果系数有解,则这个挑战解就是方程的解,如果系数无解,则这个挑战解就不是方程的解)
即推动过程是随机干扰项的非齐次方程的特解
待定系数法可能误解,所以我们将一开始提出的用于尝试的解称之为挑战解
(1)简单情形1:一阶差分方程+一个随机干扰项方程为
猜想的挑战解形式为:
代入方程得

对任意的t和efshow,上述的式子都要成立,那就只能让常数项和系数都为零啦~
于是可以得到:
和

考虑到分母,还是分类讨论:
分类情形1:

这个结果和第一部分中使用向前迭代解本方程对所得的解的结果完全一致
最后我们可以配上对应的齐次方程的通解,组合成非齐次方程的通解,如下:

分类情形2:

由于efshow的求和未必有限,所以该解可能发散。于是施加如下初始条件:

最终将特解写为:

但是我觉得,由于t的存在,这个解还是发散的,所以前面施加初始条件然并卵。
(2)简单情形2:一阶差分方程+两个随机干扰项
方程为: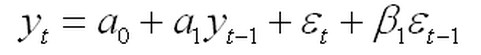
猜想的挑战解形式为: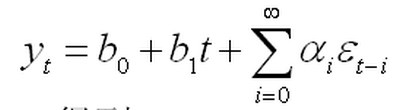
使用(1)简单情形1中的步骤和方法,不再赘述。
(3)二阶差分方程+一个随机干扰项 ,方程为: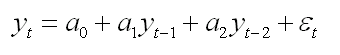
猜想的挑战解形式为:

代入方程可以得到:

和
和 (可以解出a(j))
(可以解出a(j))
 (可以解出a(j))
(可以解出a(j))
(五)滞后算子
滞后算子L:
滞后算子的性质:



利用性质5和性质6,结合性质1,就可以解出差分方程。(级数求和与展开)
如果是高阶,则可以因式分解,拆分后,再进行级数展开。