动态规划常见问题

1 0-1背包

 

 java代码：

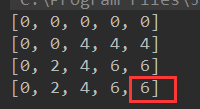
//import java.util.ArrayList;
import java.util.Arrays;

public class Solution {
    public static int[][] Bag(int W,int N, int wt[],int val[]){
        //初始化dp数组-定义状态
        /*dp[i][w] 表⽰：对于前 i 个物品，当前背包的容量为 w 时，这种情况下可以装下的最⼤价值是 dp[i][w]*/
        int dp[][] = new int[N+1][W+1];
        for (int i = 0; i < dp.length; i++) {
            Arrays.fill(dp[i],0);
        }
        //编写状态转移代码
        for (int i = 1; i <= N; i++) {
            for (int w = 1; w <= W; w++) {
                if(w - wt[i-1] < 0){//容量不够，此时不装
                    dp[i][w] = dp[i-1][w];
                }else{//容量够，装入背包
                    dp[i][w]=Math.max(dp[i-1][w],//如果你没有把这第 i 个物品装⼊背包
                                      dp[i-1][w-wt[i-1]] + val[i-1]);//如果你把这第 i 个物品装⼊了背包
                }
            }
        }
        //返回dp表
        return dp;
    }

    public static void main(String[] args) {
        int wt[] = new int[]{2,1,3};
        int val[] = new int[]{4,2,3};
        int W = 4,N = 3;

        int res[][] = Bag(W,N,wt,val);
        for (int i = 0; i < res.length; i++) {
            System.out.println(Arrays.toString(res[i]));
        }
    }
}

结果：