动态规划（一）：矩阵取数问题

一、问题描述：

给定一个m行n列的矩阵，矩阵每个元素是一个正整数，你现在在左上角（第一行第一列），你需要走到右下角（第m行，第n列），每次只能朝右或者下走到相邻的位置，不能走出矩阵。走过的数的总和作为你的得分，求最大的得分。

   

二、分析：

1. 定义

   二维数组A[][]表示矩阵（下标从1开始）

   f(int x,int y)表示从起点到第x行第y列的最优路径上的数之和

   

1. 递推式：

   

   

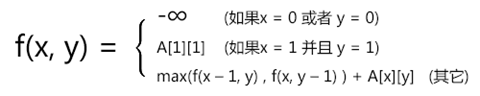
① 下标从1开始，第0行或第0列不存在

② f(1, 1)是起点，没得选

③ 从起点达到(x,y)的最优路径要经过(x – 1,y)或者(x,y – 1)，从起点到达(x – 1,y)或者(x,y – 1)的路径一定也必须是最优的。二者中取较大的

1. 列表

   

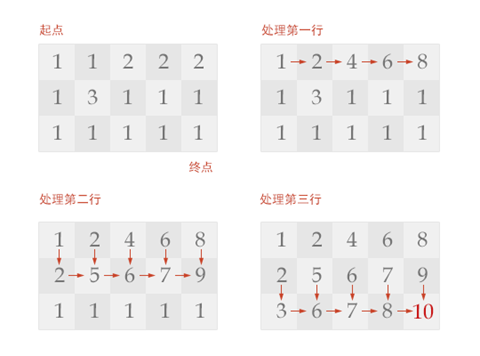
   最大得分只有一个，但最优路径不是唯一的：当f(x – 1,y) ＝ f(x, y – 1)时，前一个位置在上面或者左面都可以（得到的分数都是最大），所以路径还是很多很多的

2. 复杂度：

   时间复杂度和空间复杂度都是O(m*n)

三、例题

1. 题目

   输入

   第1行：N，N为矩阵的大小。(2 <= N <= 500)

   第2 - N + 1行：每行N个数，中间用空格隔开，对应格子中奖励的价值。（1 <= N[i] <= 10000)

      

   输出

   输出能够获得的最大价值。

      

   输入示例

   3

   1 3 3

   2 1 3

   2 2 1

      

   输出示例

   11

2. 代码

   import java.util.*;

      

   public class Main {

   public static void main(String[] args) {

   /* 输入 */

   Scanner sc = new Scanner(System.in);

   int n = sc.nextInt();

   int[][] arr = new int[n+1][n+1];

   int[][] max = new int[n+1][n+1];

      

   for(int i = 1; i <= n ; i++){

   for (int j = 1; j <= n; j++) {

   arr[i][j] = sc.nextInt();//赋值给某个变量

   }

   }

   for(int i = 1; i <= n ; i++){

   for (int j = 1; j <= n; j++) {

   if (i == 1 && j == 1){

   max[i][j] = arr[i][j];

   }

   else{

   max[i][j] = Math.max(max[i-1][j],max[i][j-1])+arr[i][j];

   }

   }

   }

   System.out.println(max[n][n]);

   }

   }