poj 2352 stars 线段树

Stars

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 40026		Accepted: 17373

Description

Astronomers often examine star maps where stars are represented by points on a plane and each star has Cartesian coordinates. Let the level of a star be an amount of the stars that are not higher and not to the right of the given star. Astronomers want to know the distribution of the levels of the stars.

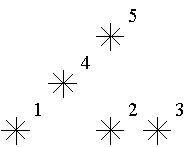
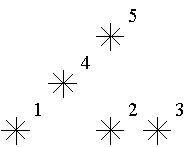
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it's formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.

You are to write a program that will count the amounts of the stars of each level on a given map.

Input

The first line of the input file contains a number of stars N (1<=N<=15000). The following N lines describe coordinates of stars (two integers X and Y per line separated by a space, 0<=X,Y<=32000). There can be only one star at one point of the plane. Stars are listed in ascending order of Y coordinate. Stars with equal Y coordinates are listed in ascending order of X coordinate.

Output

The output should contain N lines, one number per line. The first line contains amount of stars of the level 0, the second does amount of stars of the level 1 and so on, the last line contains amount of stars of the level N-1.

Sample Input

5
1 1
5 1
7 1
3 3
5 5

Sample Output

1
2
1
1
0

Hint

This problem has huge input data,use scanf() instead of cin to read data to avoid time limit exceed.

题目大意：

给你n个点代表n个星星，以该点为起点向x，y轴作垂线，会得到一个矩形，这个矩形里面所包含的星星数（不包括它本身）称为该星星的等级

，要求输出在0-n-1等级各有多少个星星。注意给出的点的顺序很有讲究，是按照y坐标升序给出，如果y坐标相同，则按照x坐标升序给出，题目

这样说就相当于减少了这个题目的难度，如果题目没有给出这样的提示，我们也需要这样进行处理。

线段树菜鸟总结：因为才刚刚接触线段树，我是再看ppt学线段树的过程中看到了这一道题目，所以才过来做了一下，如果让我自己去做，十有八九是

做不出来的，毕竟线段树才做了两道题，借这一道题也顺便说一下我的拙见吧。刚开始学的线段树是包含三个函数，build函数，change(update)函数

find函数，进行基本的线段树建立，查询，更新，这个模板也让我解决了一小部分题目，如hdu1166(敌兵布阵），hdu1754(I hate it)，这两道题

目对线段树使用的提示太明显了，线段容易寻找，如军营编号，学生编号，而且输出也是围绕对某个叶子节点的更改或者是对某一个区间的查询，同时

子节点与父节点的关系也相当明显，如父节点等于左右子节点之和或左右子节点中最大值，实践才是进步的阶梯，尽管有模板，但在做这两道题的过程中

还是出现了一些问题，自己对函数参数的理解更加深刻了一些，同时也知道tree数组应该开多大（TLE的我好痛），也有几点优化小技巧，比如：

tips 1:在线建树--即不开线段树组 ，边输入边建树，这样可以节省一定的内存.

tips 2:线段树进行的各种功能都是围绕二分思想，在*2，/2的时候可以用>>1,<<1来代替，可以缩短时间。

做完了这两道题，内心还是有一丢丢得意，以为已经基本掌握了线段树，然而我又做了这一道stars,才知道自己才是图样图森破，orz,线段树博大精深，那

两道水题只是敲门砖。。。线段树灵活的多，离掌握线段树我还有着很远的距离。

本道题思路分析：首先要发现这道题的特点，数据非常大，暴力做必死，因为坐标是按照y升序给出，这就保证了先前的星星的所构成的矩形中部可能包含

后给出的星星，这样就可以边建树边查找，更新level数组，这与我之前做的那两道题就有着区别了，另外两道题是先将树建好，然后再进行查找更新操作，

然这道题绝对不能这么做，因为线段树是一维的，然而坐标本来是两维的，这道题之所以能够使用线段树，是因为y坐标按升序给出，这样也就不用考虑

y坐标了，如果是先建树后查找就会出现问题，虽然x坐标大，但是y坐标未必是最大的，这样就会出错，因此必须要边建树边查找，这样就可以保证后面

给出的点不会影响查找结果的正确性。好神奇。。orz，同时区别于那两道题，那两道题不管是学生序号还是军营序号都是明确从1-n，所以可以直接数组

储存，进行建树，但是这道题x坐标未必是连续的，这就要求我们定向建树，所以在build函数里面加了一个参数x，来进行定向建树。。orz

这都是新姿势。。。orz 继续努力

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=32000+100;
int x[maxn],tree[4*maxn];
int level[15000+50];//储存不同level的星星个数
void build(int p,int l,int r,int x)//x来界定建哪一个位置的树,该函数既是建树也是对树的更新
{
    if(l==r) {tree[p]++;return;}//节点的含义，该位置有一个星星（0或1）
    int mid=(l+r)/2;
    if(mid>=x) build(2*p,l,mid,x);
    else build(2*p+1,mid+1,r,x);
    tree[p]=tree[2*p]+tree[2*p+1];//这个区间内星星的个数
}
int find(int p,int l,int r,int x,int y)
{
    if(l<=x&&r<=y) {return tree[p];}
    int mid=(l+r)/2;
    if(y<=mid) return find(2*p,l,mid,x,y);
    if(x>mid) return find(2*p+1,mid+1,r,x,y);
    else return find(2*p,l,mid,x,mid)+find(2*p+1,mid+1,r,mid+1,y);
}
int main()
{
    int n,y,maxn=-1;
    scanf("%d",&n);
    memset(tree,0,sizeof(tree));
    memset(level,0,sizeof(level));
    for(int i=1;i<=n;i++)
    {
    scanf("%d%d",&x[i],&y);
    if(x[i]>maxn) maxn=x[i];//用maxn来作为线段树边界
    }
    for(int i=1;i<=n;i++)
    {
        build(1,0,maxn,x[i]);
        level[find(1,0,maxn,0,x[i])-1]++;
    }
    for(int i=0;i<n;i++)
        printf("%d ",level[i]);
    return 0;
}

代码：