转自:https://blog.csdn.net/Orange_Spotty_Cat/article/details/80499031 略有改动,仅供个人学习使用
简介
ROC曲线与AUC面积均是用来衡量分类型模型准确度的工具。通俗点说,ROC与AUC是用来回答这样的问题的:
- 分类模型的预测到底准不准确?
- 我们建出模型的错误率有多大?正确率有多高?
- 两个不同的分类模型中,哪个更好用?哪个更准确?
一句话概括版本:
ROC是一条线,如果我们选择用ROC曲线评判模型的准确性,那么越靠近左上角的ROC曲线,模型的准确度越高,模型越理想;
AUC是线下面积,如果我们选择用AUC面积评判模型的准确性,那么模型的AUC面积值越大,模型的准确度越高,模型越理想;
数据分析与挖掘体系位置
ROC曲线与AUC面积都是评判模型结果的指标,因此属于模型评估的一部分。此外,ROC曲线与AUC面积均多用于判断分类器(Classifier)的优劣,因此适用于分类型的数据模型,如分类树(Classification Tree)、逻辑回归(Logistic Regression)、线性判别分析(Linear Discriminant Analysis)等方法。
在分类型模型评判的指标中,常见的方法有如下三种:
混淆矩阵(也称误差矩阵,Confusion Matrix)
ROC曲线
AUC面积
本篇主要介绍第二与第三种方法,即ROC曲线与AUC面积。
此方法在整个数据分析与挖掘体系中的位置如下图所示。

ROC曲线的定义
ROC曲线全称为受试者工作特征曲线(Receiver Operating Characteristic Curve)。虽然听上去很高端,但是ROC其实非常容易理解。一句话说,ROC就是一张图上的曲线,我们通过曲线的形状来判定模型的好坏。
那么要想了解一个曲线代表什么意思,首先最好搞明白曲线的横轴与纵轴分别代表什么。
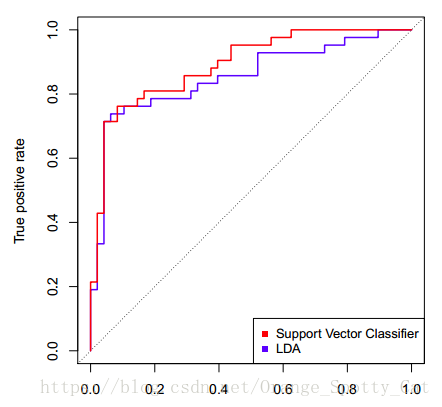
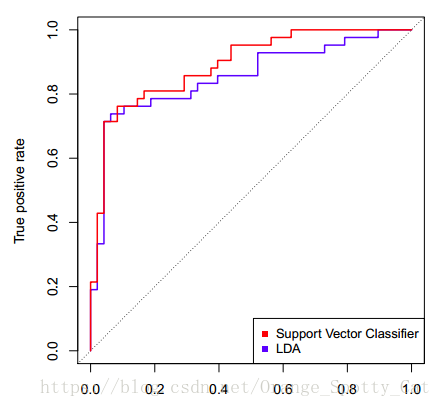
上图中显示的是两条ROC曲线,一条蓝色,一条红色。他们分别对应两个不同的模型。我们可以看到,图中横轴写着“False positive rate”,纵轴写着“True positive rate”。
这两个就是ROC曲线绘制的关键:我们通过计算分类模型的“False positive rate”与“True positive rate”值,分别把它们当成横纵轴,就能够绘制出这个模型的ROC曲线。
那么,怎么计算这两个指标呢?
ROC曲线的计算
ROC曲线的横轴与纵轴,与混淆矩阵(Confusion Matrix)有着密切的关系,具体的理解请详见混淆矩阵篇的讲解。这里只是简单回顾一下:
在分类型模型中,以二分类为例,我们的模型结果一般可以视为0/1问题,或者说positive/negative的问题。模型的产出物,不是positive,就是negative。
我们通过样本的采集,能够直接知道真实的情况下,哪些数据结果是positive,哪些结果是negative。同时,我们通过用样本数据跑出分类型模型的结果,也可以知道模型认为这些数据哪些是positive,哪些是negative。
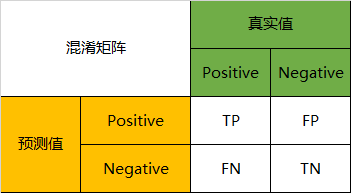
因此,我们就能得到这样四个结果:
真实值是positive,模型认为是positive的数量(True Positive=TP)
真实值是positive,模型认为是negative的数量(False Negative=FN)
真实值是negative,模型认为是positive的数量(False Positive=FP)
真实值是negative,模型认为是negative的数量(True Negative=TN)
将这四种结果一起呈现在表格中,就能得到如下这样一个矩阵,我们称它为混淆矩阵(Confusion Matrix):
从名字上就能看出,ROC的横纵轴计算方式是与混淆矩阵有着密切关系的。
横轴(False positive rate)的计算:
横轴的指标,在英文中被称为False positive rate,简称FPR。
FPR可以被理解为:在所有真实值为Negative的数据中,被模型错误的判断为Positive的比例。其计算公式为:
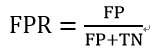
纵轴(True Positive Rate)的计算:
纵轴的指标,在英文中被称为True Positive Rate,简称TPR。
TPR可以被理解为:在所有真实值为Positive的数据中,被模型正确的判断为Positive的比例。其计算公式为:
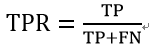
ROC曲线的解读
FPR与TPR分别构成了ROC曲线的横纵轴,因此我们知道在ROC曲线中,每一个点都对应着模型的一次结果。
- 如果ROC曲线完全在纵轴上,代表这一点上,x=0,即FPR=0。模型没有把任何negative的数据错误的判为positive,预测完全准确。这是真正的大牛模型,我是做不出来了。
- 如果ROC曲线完全在横轴上,代表这一点上,y=0,即TPR=0。模型没有把任何positive的数据正确的判断为positive,预测完全不准确。平心而论,这种模型能做出来也是蛮牛的,因为模型真正做到了完全不准确,所以只要反着看结果就好了嘛。
- 所以如果ROC曲线完全与右上方45度倾角线重合,证明模型的准确率是正好50%,错判的几率是一半一半。
因此,我们绘制出来ROC曲线的形状,是希望TPR大,而FPR小。因此对应在图上就是曲线尽量往左上角贴近。45度的直线一般被常用作Benchmark,即基准模型,我们的预测分类模型的ROC要能优于45度线,否则我们的预测还不如50/50的猜测来的准确。
所以,回到下图。从整个图上看,红色的ROC线更靠近左上方。因此,红色线代表的SVM分类器的表现要整体优于蓝色线代表的LDA分类器。
ROC曲线的绘制
我们已经知道,ROC曲线中的每一个点就能代表一次预测的结果。那么整条ROC的曲线是如何绘制的呢?
答案就是:ROC曲线上的一系列点,代表选取一系列的阈值(threshold)产生的结果。
在分类问题中,我们模型预测的结果不是negative/positive。而是一个negatvie或positive的概率。那么在多大的概率下我们认为观测值应该是negative或positive呢?这个判定的值就是阈值(threshold)。
ROC曲线上众多的点,每个点都对应着一个阈值的情况下模型的表现。多个点连起来就是ROC曲线了。
AUC的定义与解读
AUC的英文叫做Area Under Curve,即曲线下的面积,不能再直白。它就是值ROC曲线下的面积是多大。每一条ROC曲线对应一个AUC值。AUC的取值在0与1之间。
- AUC = 1,代表ROC曲线在纵轴上,预测完全准确。不管Threshold选什么,预测都是100%正确的。
- 0.5 < AUC < 1,代表ROC曲线在45度线上方,预测优于50/50的猜测。需要选择合适的阈值后,产出模型。
- AUC = 0.5,代表ROC曲线在45度线上,预测等于50/50的猜测。
- 0 < AUC < 0.5,代表ROC曲线在45度线下方,预测不如50/50的猜测。
- AUC = 0,代表ROC曲线在横轴上,预测完全不准确。
【补充】ROC曲线和AUC面积理解
转自: https://blog.csdn.net/program_developer/article/details/79946787 略有改动,仅供个人学习使用
目录:
(1) ROC曲线的由来
(2) 什么是ROC曲线
(3) ROC曲线的意义
(4) AUC面积的由来
(5) 什么是AUC面积
(6) AUC面积的意义
(7) 讨论:在多分类问题下能不能使用ROC曲线
一、 ROC曲线的由来
很多学习器是为测试样本产生一个实值或概率预测,然后将这个预测值与一个分类阈值进行比较,若大于阈值则分为正类,否则为反类。例如,神经网络在一般情形下是对每个测试样本预测出一个[0.0,1.0]之间的实值,然后将这个值与阈值0.5进行比较,大于0.5则判为正例,否则为反例。这个阈值设置的好坏,直接决定了学习器的泛化能力。
在不同的应用任务中,我们可根据任务需求来采用不同的阈值。例如,若我们更重视“查准率”,则可以把阈值设置的大一些,让分类器的预测结果更有把握;若我们更重视“查全率”,则可以把阈值设置的小一些,让分类器预测出更多的正例。因此,阈值设置的好坏,体现了综合考虑学习器在不同任务下的泛化性能的好坏。为了形象的描述这一变化,在此引入ROC曲线,ROC曲线则是从阈值选取角度出发来研究学习器泛化性能的有力工具。
二、 什么是ROC曲线
ROC全称是“受试者工作特征”(Receiver OperatingCharacteristic)曲线。我们根据学习器的预测结果,把阈值从0变到最大,即刚开始是把每个样本作为正例进行预测,随着阈值的增大,学习器预测正样例数越来越少,直到最后没有一个样本是正样例。在这一过程中,每次计算出两个重要量的值,分别以它们为横、纵坐标作图,就得到了“ROC曲线”。
ROC曲线的纵轴是“真正例率”(True Positive Rate, 简称TPR),横轴是“假正例率”(False Positive Rate,简称FPR):
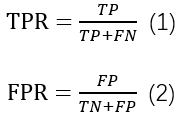
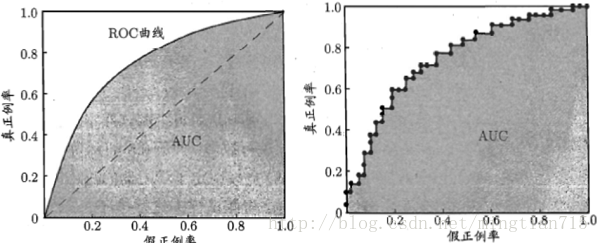
显示ROC曲线的图称为“ROC图”。图1给出了一个示意图,显然,对角线对应于“随机猜测”模型,而点(0,1)则对应于将所有正例预测为真正例、所有反例预测为真反例的“理想模型”。

现实任务中通常是利用有限个测试样例来绘制ROC图,此时仅能获得有限个(真正例率,假正例率)坐标对,无法产生图1中的光滑ROC曲线,只能绘制出图2所示的近似ROC曲线。绘制过程很简单:给定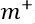 个正例和
个正例和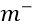 个反例,根据学习器预测结果对样例进行排序,然后把分类阈值设置为最大,即把所有样例均预测为反例,此时真正例率和假正例率均为0,在坐标(0,0)处标记一个点。然后,将分类阈值依次设为每个样例的预测值,即依次将每个样例划分为正例。设前一个标记点坐标为
个反例,根据学习器预测结果对样例进行排序,然后把分类阈值设置为最大,即把所有样例均预测为反例,此时真正例率和假正例率均为0,在坐标(0,0)处标记一个点。然后,将分类阈值依次设为每个样例的预测值,即依次将每个样例划分为正例。设前一个标记点坐标为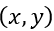 ,当前若为真正例,则对应标记点的坐标为
,当前若为真正例,则对应标记点的坐标为 ;当前若为假正例,则对应标记点的坐标为
;当前若为假正例,则对应标记点的坐标为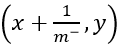 ,然后用线段连接相邻点即得。
,然后用线段连接相邻点即得。
三、 ROC曲线的意义
(1)主要作用
1. ROC曲线能很容易的查出任意阈值对学习器的泛化性能影响。
2.有助于选择最佳的阈值。ROC曲线越靠近左上角,模型的查全率就越高。最靠近左上角的ROC曲线上的点是分类错误最少的最好阈值,其假正例和假反例总数最少。
3.可以对不同的学习器比较性能。将各个学习器的ROC曲线绘制到同一坐标中,直观地鉴别优劣,靠近左上角的ROC曲所代表的学习器准确性最高。
(2)优点
1. 该方法简单、直观、通过图示可观察分析方法的准确性,并可用肉眼作出判断。ROC曲线将真正例率和假正例率以图示方法结合在一起,可准确反映某种学习器真正例率和假正例率的关系,是检测准确性的综合代表。
2. 在生物信息学上的优点:ROC曲线不固定阈值,允许中间状态的存在,利于使用者结合专业知识,权衡漏诊与误诊的影响,选择一个更加的阈值作为诊断参考值。
四、 AUC面积的由来
如果两条ROC曲线没有相交,我们可以根据哪条曲线最靠近左上角哪条曲线代表的学习器性能就最好。但是,实际任务中,情况很复杂,如果两条ROC曲线发生了交叉,则很难一般性地断言谁优谁劣。在很多实际应用中,我们往往希望把学习器性能分出个高低来。在此引入AUC面积。
在进行学习器的比较时,若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者;若两个学习器的ROC曲线发生交叉,则难以一般性的断言两者孰优孰劣。此时如果一定要进行比较,则比较合理的判断依据是比较ROC曲线下的面积,即AUC(Area Under ROC Curve),如图1图2所示。