最小二乘法

　　今天要介绍的最小二乘法是用来做参数估计的方法，笔者把同济大学高等数学第六版下册翻了一下，觉得书中所讲句句珠玑，已经无可挑剔了，就“照本宣科”了。

　　“许多工程问题，常常需要根据两个变量的几组实验数值——实验数据，来找出这两个变量的函数关系的近似表达式，通常把这样得到的函数的近似表达式叫做经验公式，经验公式建立以后，就可以把生产或实验中所积累的某些经验提高到理论上加以分析。”

举个例子

　　为了测定道具的磨损速度，我们做这样的实验：经过一定时间（如每隔一小时）测量一次刀具的厚度，得到了一组实验数据

我们需要首先根据实验数据建立y与t之间的经验公式y=f（t），为此，可按下法处理。在直角坐标纸上去t为横坐标，y为纵坐标，描出各对数据的对应点。如下图：

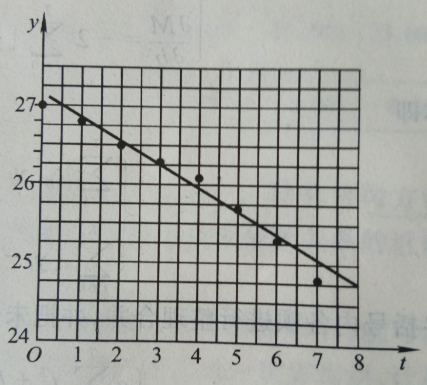
从图中可以看出，这些点的连线大致接近于一条直线，于是，就可以认为y=f（t）是线性函数，并设f（t）=at+b，其中，a和b是待估参数。下面探讨a和b如何确定

最理想的情况是所有点都位于a和b确定的直线上，但这是不可能的，因为这些点本来就不在同一条直线上。我们需要找到一条直线，使得所有点距离这条直线偏差都很小（假设所有点都不是噪点），那么如何来表示我们的需求呢？如果是偏差的和∑[y_i-f(t_i)]很小来保证每个偏差都很小呢？不能，因为偏差有正有负，在求和时，可能会互相抵消，为了避免这种情形，可对偏差去绝对值在求和，只要∑|y_i-f(t_i)|很小就能够保证每个偏差的绝对值都很小，但是还有一个不足的地方，就是这个式子中有绝对值符号，我们后面在处理这个式子的时候用到了偏微分，会很不方便，所以这里既方便处理又能表达我们需求的式子应该是这样的：M=∑[ y_i-f(t_i) ]²=∑[ y_i-(a*t_i+b) ]²，这种根据偏差的平方和为最小条件来选择常熟a、b的方法叫做最小二乘法，这种方法在机器学习中确定待估参数时是经常用到的。

　　现在我们来研究a和b满足什么条件时可使上述M最小。显然M是自变量a和b的因变量，且函数连续可导，那么我们可以通过求偏微分方程组的解来得到极值点。所以：

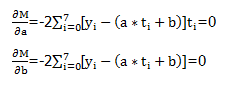
整理可得

　　

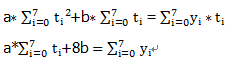
其中

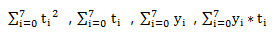
这几项是可以根据已知数据计算出来的，直接带入方程组可得a=-0.3036，b=27.125，所以经验公式为y=f(t)=-0.3036t+27.125。偏差的平方和M=0.108165，他的平方根√M=0.329，√M成为均方误差，它的大小在一定程度上反映了用经验公式来近似表达原来函数关系的近似程度的好坏。

　　这里用了一个简单的例子描述了最小二乘法的应用，在实际问题中，我们可能根本无法通过作图的方法来构建一个模型然后求解参数，一个原因是数据量太大，再者就是实际问题过于复杂以至于我们难以构建一个模型。一个可行的办法是求解n阶泰勒展开式，当然，前提是我们要拟合的公式是n阶可导的。