zoukankan html css js c++ java

第二十五篇玩转数据结构——链表（Linked List）

1.. 链表的重要性

我们之前实现的动态数组、栈、队列，底层都是依托静态数组，靠resize来解决固定容量的问题，而"链表"则是一种真正的动态数据结构，不需要处理固定容量的问题；
链表是最简单的动态数据结构；
学习链表有助于更深入的理解"引用"（或指针）；
学习链表有助于更深入的理解"递归"；
链表可以用来辅助组成其他数据结构；

2.. 链表基础

数据存储在"节点"（Node）中；
链表的形象化解释如下图：
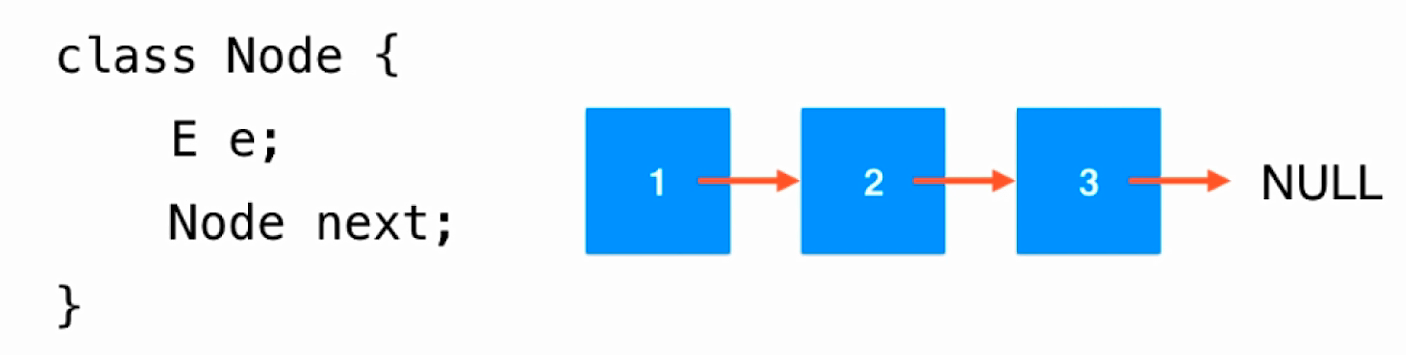
链表的优点在于，它是一种真正的动态数据结构，不需要处理固定容量问题；
链表的缺点在于，相较于数组，失去了随机访问的能力；
数组和链表的对比如下图所示：

3.. 链表的实现

实现链表的业务逻辑如下：

public class LinkedList<E> {
    private class Node {
        public E e;
        public Node next;

        //构造函数
        public Node(E e, Node next) {
            this.e = e;
            this.next = next;
        }

        //只传了参数e的构造函数
        public Node(E e) {
            this(e, null);
        }

        //不传递参数的构造函数
        public Node() {
            this(null, null);
        }

        //方便打印测试
        @Override
        public String toString() {
            return e.toString();
        }
    }

    private Node dummyHead;
    private int size;

    //构造函数
    public LinkedList() {
        dummyHead = new Node(null, null);  //虚拟头节点
        size = 0;
    }

    //获取链表中的元素个数
    public int getSize() {
        return size;
    }

    //判断链表是否为空
    public boolean isEmpty() {
        return size == 0;
    }

    //在链表的index(0-based)位置添加新的元素e
    //在链表中不是一个常用操作
    public void add(int index, E e) {
        if (index < 0 || index > size) {
            throw new IllegalArgumentException("Add failed. Illegal index.");
        }

        Node prev = dummyHead;
        for (int i = 0; i < index; i++) {
            prev = prev.next;
        }

        prev.next = new Node(e, prev.next);
        size++;
    }

    //在链表头添加新元素e
    public void addFirst(E e) {
        add(0, e);
    }

    //在链表末尾添加新的元素e
    public void addLast(E e) {
        add(size, e);
    }

    //获取链表的index(0-based)位置的元素
    //在链表中也不是一个常用操作
    public E get(int index) {
        if (index < 0 || index > size - 1) {
            throw new IllegalArgumentException("Get failed. Illegal index.");
        }

        Node cur = dummyHead.next;
        for (int i = 0; i < index; i++) {
            cur = cur.next;
        }
        return cur.e;
    }

    //获得链表的第一个元素
    public E getFirst() {
        return get(0);
    }

    //获得链表的最后一个元素
    public E getLast() {
        return get(size - 1);
    }

    //修改链表的index(0-based)位置的元素为e
    //在链表中也不是一个常用操作
    public void set(int index, E e) {
        if (index < 0 || index > size - 1) {
            throw new IllegalArgumentException("Set failed. Illegal index.");
        }

        Node cur = dummyHead.next;
        for (int i = 0; i < index; i++) {
            cur = cur.next;
        }
        cur.e = e;
    }

    //查找链表中是否存在元素e
    public boolean contains(E e) {
        Node cur = dummyHead.next;
        while (cur != null) {
            if (cur.e.equals(e)) {
                return true;
            }
            cur = cur.next;
        }
        return false;
    }

    //删除链表的index(0-based)位置的元素，并返回该元素
    //在链表中也不是一个常用操作
    public E remove(int index) {
        if (index < 0 || index > size - 1) {
            throw new IllegalArgumentException("Remove failed. Illegal index.");
        }
        Node prev = dummyHead;
        for (int i = 0; i < index; i++) {
            prev = prev.next;
        }
        Node retNode = prev.next;
        prev.next = retNode.next;
        retNode.next = null;
        size--;

        return retNode.e;
    }

    //删除链表中的第一个元素，并返回该元素
    public E removeFirst() {
        return remove(0);
    }

    //删除链表中的最后一个元素，并返回该元素
    public E removeLast() {
        return remove(size - 1);
    }

    // 从链表中删除元素e
    public void removeElement(E e){

        Node prev = dummyHead;
        while(prev.next != null){
            if(prev.next.e.equals(e))
                break;
            prev = prev.next;
        }

        if(prev.next != null){
            Node delNode = prev.next;
            prev.next = delNode.next;
            delNode.next = null;
            size --;
        }
    }


    //方便打印测试
    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
//        Node cur = dummyHead.next;
//        while (cur != null) {
//            res.append(cur + "->");
//            cur = cur.next;
//        }
        for (Node cur = dummyHead.next; cur != null; cur = cur.next) {
            res.append(cur + "->");
        }
        res.append("NULL");

        return res.toString();
    }
}

测试的业务逻辑如下：

public class Main {

    public static void main(String[] args) {
        LinkedList<Integer> linkedList = new LinkedList<>();
        for (int i = 0; i < 5; i++) {
            linkedList.addFirst(i);
            System.out.println(linkedList);
        }

        linkedList.add(2, 666);
        System.out.println(linkedList);

        linkedList.remove(2);
        System.out.println(linkedList);

        linkedList.removeFirst();
        System.out.println(linkedList);

        linkedList.removeLast();
        System.out.println(linkedList);
    }
}

输出结果：

0->NULL
1->0->NULL
2->1->0->NULL
3->2->1->0->NULL
4->3->2->1->0->NULL
4->3->666->2->1->0->NULL
4->3->2->1->0->NULL
3->2->1->0->NULL
3->2->1->NULL

4.. 链表的时间复杂度分析：

添加操作 O(n)

addLast(e)     O(n)
addFirst(e)    O(1)
add(index, e)  O(n/2)=O(n)

删除操作 O(n)

removeLase(e)     O(n)
removeFirst(e)    O(1)
remove(index, e)  O(n/2)=O(n)

修改操作 O(n)
```
set(index, e)  O(n)
```
查找操作 O(n)
```
get(index)   O(n)
contains(e)  O(n)
```
总体来说，链表的增、删、改、查的时间复杂度都是O(n)
如果我们只对链表的头进行添加和删除操作，那么时间复杂度是O(1)，如果我们只查链表头的元素，那么时间复杂度也是O(1)，满足这些条件的数据结构，我们很容易就会想到"栈"，对于"栈"而言，遵循后进先出的原则，只对栈的一端，也就是"栈顶"进行操作，无论是添加、删除还是查看元素，都在栈顶进行。所以，我们就可以把链表头当作栈顶，用链表来作为栈的底层实现，来实现出一个栈。

5.. 使用链表来实现一个"栈"

链表栈的实现及测试的业务逻辑如下：

public class LinkedListStack<E> implements Stack<E> {

    private LinkedList<E> list;

    //构造函数
    public LinkedListStack() {
        list = new LinkedList<>();
    }

    //实现getSize方法
    @Override
    public int getSize() {
        return list.getSize();
    }

    //实现isEmpty方法
    @Override
    public boolean isEmpty() {
        return list.isEmpty();
    }

    //实现push方法
    @Override
    public void push(E e) {
        list.addFirst(e);
    }

    //实现pop方法
    @Override
    public E pop() {
        return list.removeFirst();
    }

    //实现peek方法
    @Override
    public E peek() {
        return list.getFirst();
    }

    //方便打印测试
    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append("Stack: top ");
        res.append(list);
        return res.toString();
    }

    //测试
    public static void main(String[] args) {

        LinkedListStack<Integer> stack = new LinkedListStack<>();
        //测试入栈push
        for (int i = 0; i < 5; i++) {
            stack.push(i);
            System.out.println(stack);
        }
        //测试出栈
        stack.pop();
        System.out.println(stack);
    }
}

输出结果：

Stack: top 0->NULL
Stack: top 1->0->NULL
Stack: top 2->1->0->NULL
Stack: top 3->2->1->0->NULL
Stack: top 4->3->2->1->0->NULL
Stack: top 3->2->1->0->NULL

6.. 数组栈与链表栈的性能比较

测试的业务逻辑如下：

import java.util.Random;

public class Main {

    //测试使用stack运行opCount个push和pop操作所需的时间，单位：秒
    private static double testStack(Stack<Integer> stack, int opCount) {

        long startTime = System.nanoTime();

        Random random = new Random();
        for (int i = 0; i < opCount; i++) {
            stack.push(random.nextInt(Integer.MAX_VALUE));
        }
        for (int i = 0; i < opCount; i++) {
            stack.pop();
        }

        long endTime = System.nanoTime();
        return (endTime - startTime) / 1000000000.0;
    }

    public static void main(String[] args){
        int opCount = 10000;

        ArrayStack<Integer> arrayStack = new ArrayStack<>();
        double time1 = testStack(arrayStack,opCount);
        System.out.println("ArrayStack, time: " + time1 + " s");

        LinkedListStack<Integer> linkedListStack = new LinkedListStack<>();
        double time2 = testStack(linkedListStack,opCount);
        System.out.println("LinkedListStack, time: " + time2 + " s");

        // 这二者的时间比较很复杂，ArrayStack会在扩容和缩容操作上面耗费时间，LinkedListStack则会在创建新的Node上面耗费时间
    }
}

这两种栈的时间复杂度基本处于相同的水平

7.. 使用链表实现一个"队列"

链表队列的实现及测试的业务逻辑如下

public class LinkListQueue<E> implements Queue<E> {

    private class Node {
        public E e;
        public Node next;

        public Node(E e, Node next) {
            this.e = e;
            this.next = next;
        }

        public Node(E e) {
            this(e, null);
        }

        public Node() {
            this(null, null);
        }

        @Override
        public String toString() {
            return e.toString();
        }
    }

    private Node head, tail;
    private int size;

    public LinkListQueue() {
        head = null;
        tail = null;
        size = 0;
    }

    //实现getSize
    @Override
    public int getSize() {
        return size;
    }

    //实现isEmpty
    @Override
    public boolean isEmpty() {
        return size == 0;
    }

    //实现enqueue
    @Override
    public void enqueue(E e) {
        if (tail == null) {
            tail = new Node(e);
            head = tail;
        } else {
            tail.next = new Node(e);
            tail = tail.next;
        }
        size++;
    }

    //实现dequeue
    @Override
    public E dequeue() {
        if (isEmpty()) {
            throw new IllegalArgumentException("Cannot dequeue from an empty queue.");
        }
        Node retNode = head;
        head = head.next;
        retNode.next = null;
        if (head == null) {
            tail = null;
        }
        size--;
        return retNode.e;
    }

    //实现getFront
    public E getFront() {
        if (isEmpty()) {
            throw new IllegalArgumentException("Queue is empty.");
        }
        return head.e;
    }

    //方便打印测试
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append("Queue: front ");

        Node cur = head;
        while (cur != null) {
            res.append(cur + "->");
            cur = cur.next;
        }
        res.append("NULL");
        return res.toString();
    }

    //测试
    public static void main(String[] args) {
        LinkListQueue<Integer> queue = new LinkListQueue<>();
        for (int i = 0; i < 6; i++) {
            queue.enqueue(i);
            System.out.println(queue);

            if (i % 3 == 2) {
                queue.dequeue();
                System.out.println(queue);
            }
        }
    }
}

输出结果：

Queue: front 0->NULL
Queue: front 0->1->NULL
Queue: front 0->1->2->NULL
Queue: front 1->2->NULL
Queue: front 1->2->3->NULL
Queue: front 1->2->3->4->NULL
Queue: front 1->2->3->4->5->NULL
Queue: front 2->3->4->5->NULL

8.. 数组队列、循环队列和链表队列的性能比较

测试的业务逻辑如下：

import java.util.Random;

public class Main {

    // 测试使用q运行opCount个enqueue和dequeue操作所需要的时间，单位：秒
    private static double testQueue(Queue<Integer> q, int opCount) {
        long startTime = System.nanoTime();

        Random random = new Random();
        for (int i = 0; i < opCount; i++) {
            q.enqueue(random.nextInt(Integer.MAX_VALUE));
        }
        for (int i = 0; i < opCount; i++) {
            q.dequeue();
        }

        long endTime = System.nanoTime();
        return (endTime - startTime) / 1000000000.0;
    }

    public static void main(String[] args) {

        int opCount = 100000;

        ArrayQueue<Integer> arrayQueue = new ArrayQueue<>();
        double time1 = testQueue(arrayQueue, opCount);
        System.out.println("ArrayQueue, time: " + time1 + " s");

        LoopQueue<Integer> loopQueue = new LoopQueue<>();
        double time2 = testQueue(loopQueue, opCount);
        System.out.println("LoopQueue, time: " + time2 + " s");

        LinkListQueue<Integer> linkListQueue = new LinkListQueue<>();
        double time3 = testQueue(linkListQueue, opCount);
        System.out.println("LinkListQueue, time: " + time3 + " s");

    }
}

输出结果：

ArrayQueue, time: 3.069366801 s
LoopQueue, time: 0.010702659 s
LinkListQueue, time: 0.007079073 s

9.. 小练习，删除掉链表中所有值为val的节点

不使用dummyHead的实现方法

class Solution {
    public ListNode removeElements(ListNode head, int val) {

        while (head != null && head.val == val) {
            //head = head.next;
            ListNode delNode = head;
            head = head.next;
            delNode.next = null;
        }

        if (head == null) {
            return null;
        }

        ListNode prev = head;
        while (prev.next != null) {
            if (prev.next.val == val) {
                //prev.next = prev.next.next;
                ListNode delNode = prev.next;
                prev.next = delNode.next;
                delNode.next = null;
            } else {
                prev = prev.next;
            }
        }

        return head;
    }
}

使用dummyHead的实现方法：

class Solution2 {
    public ListNode removeElements(ListNode head, int val) {

        ListNode dummyHead = new ListNode(-1);
        dummyHead.next = head;

        ListNode prev = dummyHead;
        while (prev.next != null) {
            if (prev.next.val == val) {
                //prev.next = prev.next.next;
                ListNode delNode = prev.next;
                prev.next = delNode.next;
                delNode.next = null;
            } else {
                prev = prev.next;
            }
        }

        return dummyHead.next;
    }
}

使用dummyHead之后，代码变得更加简洁

10.. 递归

从本质上讲，递归，就是将原来的问题转化为更小的同一个问题；
递归举例，数组求和：

Sum(arr[0...n-1]) = arr[0] + Sum(arr[1...n-1])   <-- 转化为更小的同一个问题
Sum(arr[1...n-1]) = arr[1] + Sum(arr[2...n-1])   <-- 转化为更小的同一个问题
           ......
Sum(arr[n-1...n-1]) = arr[n-1] + Sum([])   <-- 最基本的问题

代码简单实现：

public class Sum {
    public static int sum(int[] arr) {
        return sum(arr, 0);
    }

    //计算arr[l...n)这个区间内所有数的和
    private static int sum(int[] arr, int l) {
        if (l == arr.length) {        //  <--  求解最基本问题
            return 0;
        }
        return arr[l] + sum(arr, l + 1);   //  <-- 将原问题简化为更小的问题
    }

    //测试
    public static void main(String[] args) {
        int[] arr = {1, 2, 3, 4, 5, 6, 7, 8};
        System.out.println(sum(arr));
    }
}

2.. 链表的天然递归性

通过下图，很容易理解为什么链表具有天然的递归性
用递归的思想解决删除链表中的节点的问题，原理示意图：
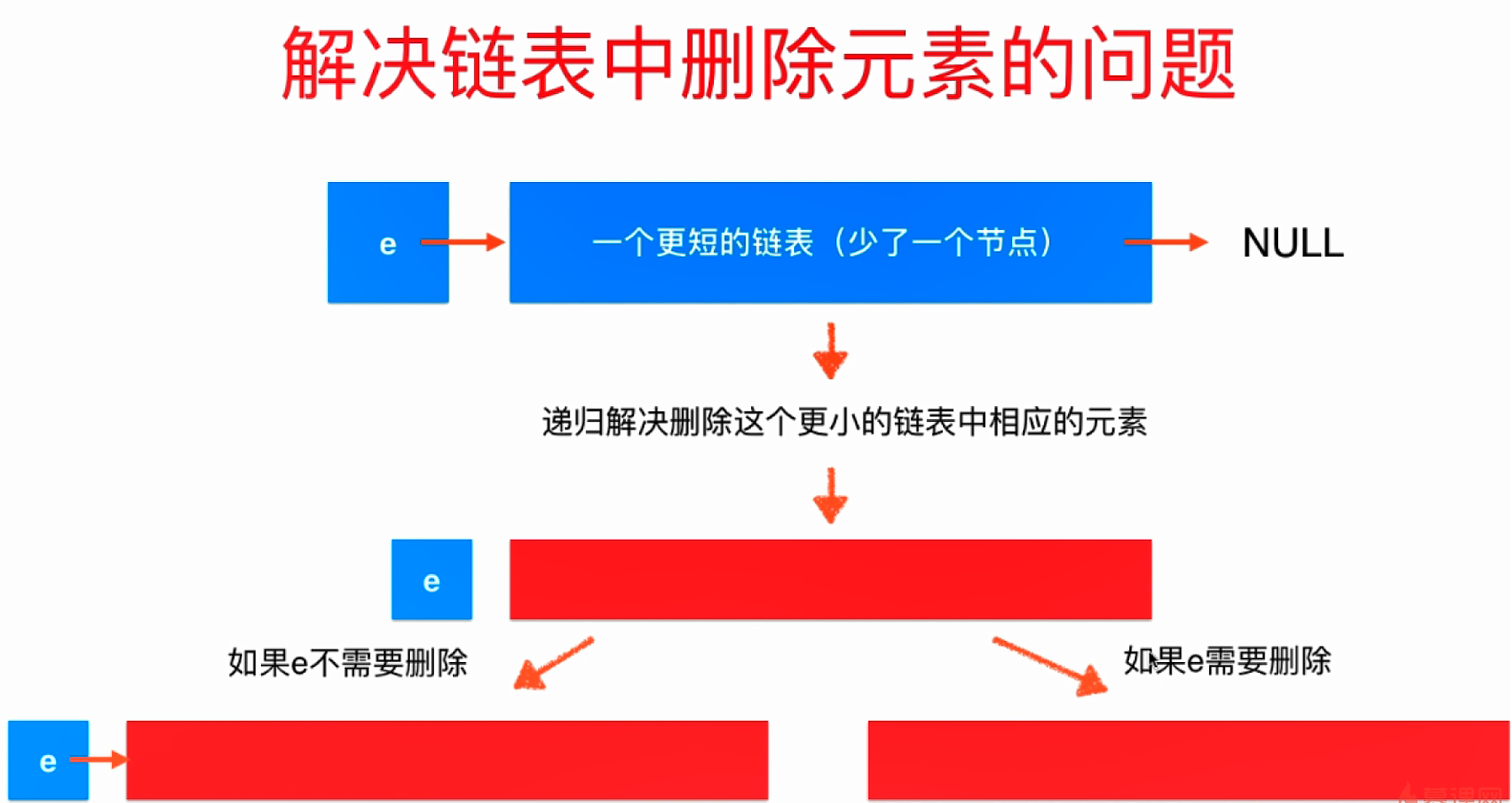
用递归实现删除链表中所有包含指定元素的节点的业务逻辑：

class Solution3 {

    public ListNode removeElements(ListNode head, int val) {
        if (head == null) {
            return null;
        }

        head.next = removeElements(head.next, val);

        //return head.val == val ? head.next : head;
        if (head.val == val) {
            return head.next;
        } else {
            return head;
        }
    }
}

查看全文

相关阅读:
Linux文本检索命令grep笔记
 Linux文本检索命令grep笔记
 Linux文件查询笔记
 Linux文件查询笔记
 Linux文件默认权限和umask笔记
 Linux文件默认权限和umask笔记
 Linux关于文件的权限笔记
 Linux关于文件的权限笔记
 Linux文件操作实用笔记
 6.创建自定义菜单

原文地址：https://www.cnblogs.com/xuezou/p/9280470.html

热门文章
Spring
Tomcat
HTTP
HTTP
Spring(3.2.3)
Spring
Spring
Spring
Spring
Linux排序命令sort笔记

第二十五篇 玩转数据结构——链表（Linked List）

第二十五篇玩转数据结构——链表（Linked List）