1.. 二叉树
-
跟链表一样,二叉树也是一种动态数据结构,即,不需要在创建时指定大小。
-
跟链表不同的是,二叉树中的每个节点,除了要存放元素e,它还有两个指向其它节点的引用,分别用Node left和Node right来表示。
-
类似的,如果每个节点中有3个指向其它节点的引用,就称其为"三叉树"...
-
二叉树具有唯一的根节点。
-
二叉树中每个节点最多指向其它的两个节点,我们称这两个节点为"左孩子"和"右孩子",即每个节点最多有两个孩子。
-
一个孩子都没有的节点,称之为"叶子节点"。
-
二叉树的每个节点,最多只能有一个父亲节点,没有父亲节点的节点就是"根节点"。
-
二叉树的形象化描述如下图:
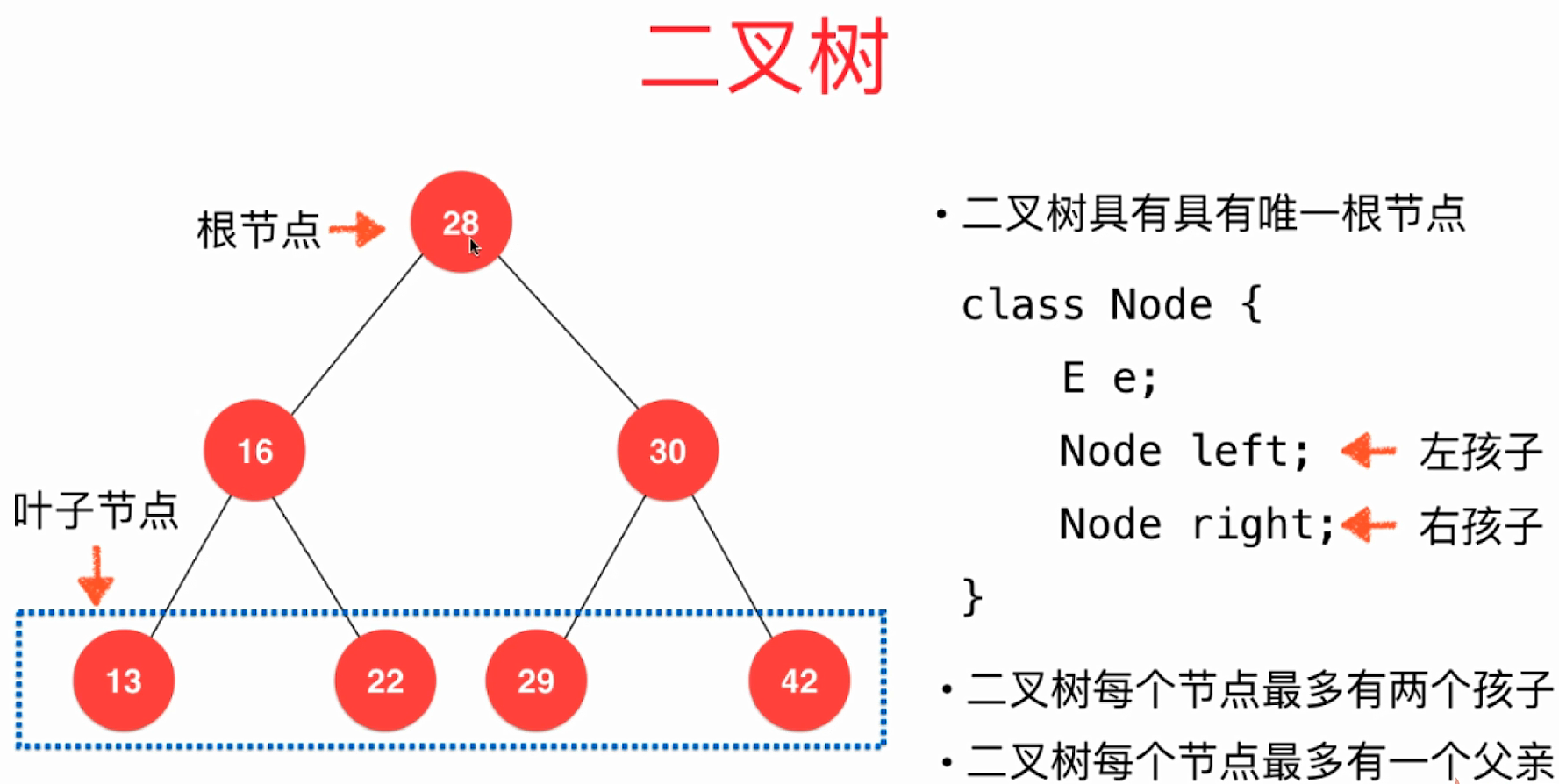
- 二叉树具有天然的递归结构。
- 每个节点的"左子树"也是一棵二叉树,每个节点的"右子树"也是一棵二叉树。
- 二叉树不一定是"满的",即,某些节点可能只有一个子节点;更极端一点,整棵二叉树可以仅有一个节点;在极端一点,整棵二叉树可以一个节点都没有;

3.. 实现二分搜索树
- 二分搜索树的构造函数、getSize方法、isEmpty方法及add方法的实现逻辑如下:
-
public class BST<E extends Comparable> { private class Node { public E e; public Node left, right; // 构造函数 public Node(E e) { this.e = e; left = null; right = null; } } private Node root; private int size; // 记录二分搜索树中存储的元素个数 public BST() { root = null; size = 0; } // 实现size方法 public int size() { return size; } // 实现isEmpty方法 public boolean isEmpty() { return size == 0; } // 实现add方法 public void add(E e) { root = add(root, e); } // 向以node为根的二分搜索树中插入元素e,递归算法 // 返回插入新节点后二分搜索树的根 private Node add(Node node, E e) { if (node == null) { size++; return new Node(e); } if (e.compareTo(node.e) < 0) { node.left = add(node.left, e); } else if (e.compareTo(node.e) > 0) { node.right = add(node.right, e); } return node; } }
- 二分搜索树的contains方法实现逻辑如下:
-
// 实现contains方法,判断二分搜索树中是否包含元素e public boolean contains(E e) { return contains(root, e); } // 判断以node为根的二分搜索树中是否包含元素e private boolean contains(Node node, E e) { if (node == null) { return false; } if (e.compareTo(node.e) == 0) { return true; } else if (e.compareTo(node.e) < 0) { return contains(node.left, e); } else { return contains(node.right, e); } }
- 二分搜索树的遍历操作,遍历操作就是把所有节点都访问一遍
- 前序遍历的业务逻辑如下:
-
//二分搜索树的前序遍历 public void preOder() { preOrder(root); } private void preOrder(Node node) { if (node == null) { return; } System.out.print(node.e); preOrder(node.left); preOrder(node.right); }
- 中序遍历的业务逻辑如下:
-
// 二分搜索树的中序遍历 public void inOrder() { inOrder(root); } // 中序遍历以node为根的二分搜索树,递归算法 private void inOrder(Node node) { if (node == null) { return; } inOrder(node.left); System.out.print(node.e); inOrder(node.right); }
- 后序遍历的业务逻辑如下:
-
// 二分搜索树的后序遍历 public void postOrder() { postOrder(root); } // 后序遍历以node为根的二分搜索树,递归算法 private void postOrder(Node node) { if (node == null) { return; } postOrder(node.left); postOrder(node.right); System.out.print(node.e); }
- 简单测试如下:
-
public class Main { public static void main(String[] args) { BST<Integer> bst = new BST<>(); int[] nums = {5, 3, 6, 8, 4, 2}; for (int num : nums) { // 测试add方法 bst.add(num); } // 测试前序遍历 bst.preOrder(); System.out.println(); // 测试中序遍历 bst.inOrder(); System.out.println(); // 测试后序遍历 bst.postOrder(); } }
- 输出结果:
-
532468 234568 243865
- 前序遍历是最自然的遍历方式,也是最常用的遍历方式;中序遍历的结果是按从小到大的顺序的排列的;后序遍历可以用于为二分搜索树释放内存。
- 利用"栈"实现二分搜索树的非递归前序遍历
-
// 二分搜索树的非递归前序遍历 public void preOrderNR() { Stack<Node> stack = new Stack<>(); stack.push(root); while (!stack.isEmpty()) { Node cur = stack.pop(); System.out.print(cur.e); if (cur.right != null) { stack.push(cur.right); } if (cur.left != null) { stack.push(cur.left); } } }
- 二分搜索树的非递归实现比递归实现更加复杂。
- 二分搜索树的前序、中序和后续遍历都属于"深度优先"算法。
- 二分搜索树的"层序遍历"属于"广度优先"算法。
- 利用"队列"实现二分搜索树的"层序遍历"
-
// 二分搜索树的层序遍历 public void levelOrder() { Queue<Node> q = new LinkedList<>(); q.add(root); while (!q.isEmpty()) { Node cur = q.remove(); System.out.print(cur.e); if (cur.left != null) { q.add(cur.left); } if (cur.right != null) { q.add(cur.right); } } }
- 获取二分搜索树中的最小元素和最大元素
-
// 寻找二分搜索树中的最小元素 public E minimum() { if (size == 0) { throw new IllegalArgumentException("BST is empty."); } return minimum(root).e; } // 返回以node为根的二分搜索树的最小元素所在节点 private Node minimum(Node node) { if (node.left == null) { return node; } return minimum(node.left); } // 寻找二分搜索树中的最大元素 public E maximum() { if (size == 0) { throw new IllegalArgumentException("BST is empty."); } return maximum(root).e; } // 返回以node为根的二分搜索树的最大元素所在节点 private Node maximum(Node node) { if (node.right == null) { return node; } return maximum(node.right); }
- 删除二分搜索树中最小元素和最大元素所在节点
-
// 从二分搜索树中删除最小元素所在节点,返回最小元素 public E removeMin() { E ret = minimum(); root = removeMin(root); return ret; } // 删除掉以node为根的二分搜索树中的最小元素所在节点 // 返回删除节点后新的二分搜索树的根 private Node removeMin(Node node) { if (node.left == null) { Node rightNode = node.right; node.right = null; size--; return rightNode; } node.left = removeMin(node.left); return node; } // 从二分搜索树中删除最大元素所在节点,返回最小元素 public E removeMax() { E ret = maximum(); root = removeMax(root); return ret; } // 删除掉以node为根的二分搜索树中的最小元素所在节点 // 返回删除节点后新的二分搜索树的根 private Node removeMax(Node node) { if (node.right == null) { Node leftNode = node.left; node.left = null; size--; return leftNode; } node.right = removeMax(node.right); return node; }
- 删除二分搜索树中指定元素所对应的节点
-
// 从二分搜索树中删除元素为e的节点 public void remove(E e) { remove(root, e); } // 删除以node为根节点的二分搜索树中元素为e的节点,递归算法 // 返回删除节点后新的二分搜索树的根 private Node remove(Node node, E e) { if (node == null) { return null; } if (e.compareTo(node.e) < 0) { node.left = remove(node.left, e); return node; } else if (e.compareTo(node.e) > 0) { node.right = remove(node.right, e); return node; } else { // 待删除节点左子树为空的情况 if (node.left == null) { Node rightNode = node.right; node.right = null; size--; return rightNode; // 待删除节点右子树为空的情况 } else if (node.right == null) { Node leftNode = node.left; node.left = null; size--; return leftNode; // 待删除节点左右子树均不为空 // 找到比待删除节点大的最小节点,即待删除节点右子树的最小节点 // 用这个节点顶替待删除节点 } else { Node successor = minimum(node.right); successor.right = removeMin(node.right); //这里进行了size--操作 successor.left = node.left; node.left = null; node.right = null; return successor; } } }