题目背景
栈是计算机中经典的数据结构,简单的说,栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作,即 pop(从栈顶弹出一个元素)和 push(将一个元素进栈)。
栈的重要性不言自明,任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时,想到了一个书上没有讲过的问题,而他自己无法给出答案,所以需要你的帮忙。
题目描述
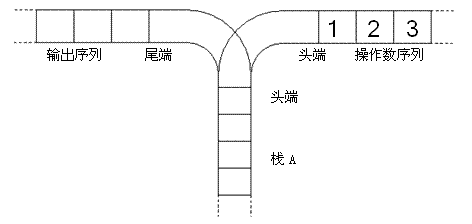
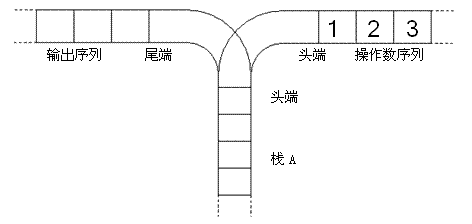
宁宁考虑的是这样一个问题:一个操作数序列,1,2,ldots ,n1,2,…,n(图示为 1 到 3 的情况),栈 A 的深度大于 nn。
现在可以进行两种操作,
- 将一个数,从操作数序列的头端移到栈的头端(对应数据结构栈的 push 操作)
- 将一个数,从栈的头端移到输出序列的尾端(对应数据结构栈的 pop 操作)
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列,下图所示为由 1 2 3 生成序列 2 3 1 的过程。
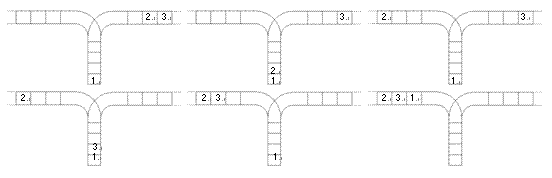
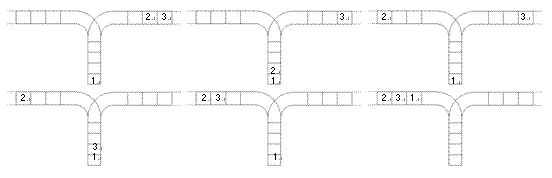
(原始状态如上图所示)
你的程序将对给定的 nn,计算并输出由操作数序列 1,2,ldots,n1,2,…,n 经过操作可能得到的输出序列的总数。
输入格式
输入文件只含一个整数 nn(1 leq n leq 181≤n≤18)。
输出格式
输出文件只有一行,即可能输出序列的总数目。
输入输出样例
输入:3
输出:5
记忆化搜索:
记忆化搜索实际上是递归来实现的,但是递归的过程中有许多的结果是被反复计算的,这样会大大降低算法的执行效率。
而记忆化搜索是在递归的过程中,将已经计算出来的结果保存起来,当之后的计算用到的时候直接取出结果,避免重复运算,因此极大的提高了算法的效率。
思路是递归搜索,由当前状态向可能的状态搜索,当前状态的结果=几个下一个状态搜索结果的和。
1 #include<bits/stdc++.h> 2 using namespace std; 3 #define MAXN 20 4 const int inf = 0x3f3f3f3f; 5 //f[i][j]:队列中还有i个元素,栈中有j个元素时的种类数 6 long n, f[20][20]; 7 long dfs(int i, int j) { 8 if (f[i][j] != 0) return f[i][j]; 9 if (i == 0) return 1;//队列为空,只有一种 10 if (j > 0) f[i][j] += dfs(i, j - 1);//栈不空时可以到达的状态 11 f[i][j] += dfs(i - 1, j + 1); 12 return f[i][j]; 13 } 14 int main() { 15 cin >> n; 16 printf("%d", dfs(n, 0)); 17 }
P1434 [SHOI2002]滑雪
题目描述
Michael 喜欢滑雪。这并不奇怪,因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael 想知道在一个区域中最长的滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子:
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度会减小。在上面的例子中,一条可行的滑坡为 2424-1717-1616-11(从 2424 开始,在 11 结束)。当然 2525-2424-2323-ldots…-33-22-11 更长。事实上,这是最长的一条。
输入格式
输入的第一行为表示区域的二维数组的行数 RR 和列数 CC。下面是 RR 行,每行有 CC 个数,代表高度(两个数字之间用 11 个空格间隔)。
输出格式
输出区域中最长滑坡的长度。
输入输出样例
5 5 1 2 3 4 5 16 17 18 19 6 15 24 25 20 7 14 23 22 21 8 13 12 11 10 9
25
说明/提示
对于 100\%100% 的数据,1leq R,Cleq 1001≤R,C≤100。
1 #include<bits/stdc++.h> 2 #define MAXN 2000 3 #define ll long long 4 using namespace std; 5 int dx[4] = { 0,0,1,-1 }; 6 int dy[4] = { 1,-1,0,0 }; 7 int n, m, a[201][201], s[201][201], ans; 8 int dfs(int x, int y) { 9 if (s[x][y])return s[x][y];//记忆化搜索 10 s[x][y] = 1;//题目中有算 11 for (int i = 0; i < 4; i++) 12 { 13 int xx = dx[i] + x; 14 int yy = dy[i] + y; 15 if (xx > 0 && yy > 0 && xx <= n && yy <= m && a[x][y] > a[xx][yy]) { 16 dfs(xx, yy); 17 s[x][y] = max(s[x][y], s[xx][yy] + 1); 18 } 19 } 20 return s[x][y]; 21 } 22 int main() 23 { 24 scanf("%d%d", &n, &m); 25 for (int i = 1; i <= n; i++) 26 for (int j = 1; j <= m; j++) 27 scanf("%d", &a[i][j]); 28 for (int i = 1; i <= n; i++) 29 for (int j = 1; j <= m; j++) 30 ans = max(ans, dfs(i, j)); 31 printf("%d", ans); 32 return 0; 33 }