余弦相似度和欧式距离的区别
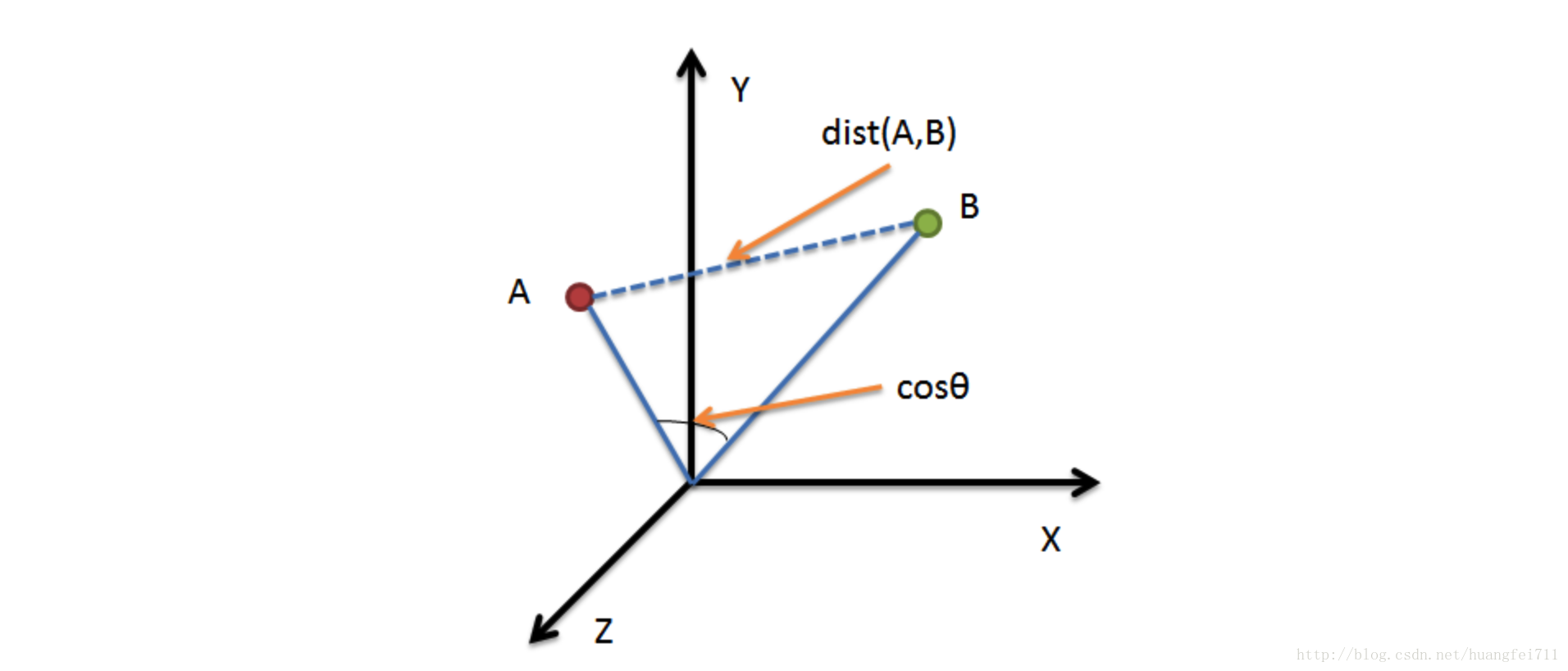
1. 计算公式
余弦相似度:
[cos left( {A,B} ight) = frac{{A cdot B}}{{{{left| A ight|}_2}{{left| B ight|}_2}}} = frac{{sumlimits_{i = 1}^n {left( {{x_i} imes {y_i}} ight)} }}{{sqrt {sumlimits_{i = 1}^n {{{left( {{x_i}} ight)}^2}} } imes sqrt {sumlimits_{i = 1}^n {{{left( {{y_i}} ight)}^2}} } }}]
欧式距离:
[distleft( {A,B} ight) = {left| {A - B} ight|_2} = sqrt {sumlimits_{i = 1}^n {{{left( {{x_i} - {y_i}} ight)}^2}} } ]
如果对向量模长进行归一化,欧式距离和余弦相似度有如下计算关系:
[{left| {A - B} ight|_2} = sqrt {2left( {1 - cos left( {A,B} ight)} ight)} ]
2. 取值范围
余弦相似度的取值范围:[-1,1]
欧式距离取值范围:[0, +∞)
3. 适用场景
余弦相似度计算的向量的夹角,它并不关心向量的绝对大小。
欧式距离体现的是数值上的绝对差异。