leetcode经典题

leetcode 31 下一个排列

实现获取下一个排列的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须原地修改，只允许使用额外常数空间。

以下是一些例子，输入位于左侧列，其相应输出位于右侧列。
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int k = -1;
        for(int i=nums.size()-2; i>=0; i--)
        {
            if(nums[i] < nums[i+1])
            {
                k = i;
                break;
            }
        }
        //cout<<k<<endl;
        if(k == -1)
        {
            sort(nums.begin(), nums.end());
        }
        else
        {
            int p = -1;
            for(int i=k+1; i<nums.size(); i++)
            {
                if(nums[i] > nums[k] && (p==-1 || nums[i] < nums[p]))
                {
                    p = i;
                }
            }        
            int tmp = nums[k];
            nums[k] = nums[p];
            nums[p] = tmp;
            sort(nums.begin()+k+1, nums.end());
        }
    }
};

leetcode 4

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。

请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2 不会同时为空。

示例 1:

nums1 = [1, 3]
nums2 = [2]

则中位数是 2.0

示例 2:

nums1 = [1, 2]
nums2 = [3, 4]

则中位数是 (2 + 3)/2 = 2.5

 

解题思路：对两个数组分别二分。

 

leetcode 5 最长回文子串

动态规划：O(n²)

Manacher算法: O(n)

leetcode 11

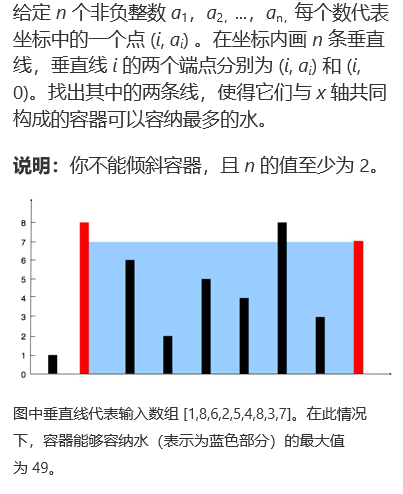
解题思路：

容量最大的容器只有两种情况：要不底长，要不高长。

我们从容器两端往回遍历，减少容器的底长，计算高长的容器就能得到最大容器。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int l = 0, r = height.size()-1, res = 0;
        while(l < r)
        {
            res = max(res, min(height[l], height[r]) * (r - l));
            if(height[l] < height[r])
            {
                l++;
            }
            else
            {
                r--;
            }
        }
        return res;
    }
};

leetcode55

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 1:

输入: [2,3,1,1,4]
输出: true
解释: 从位置 0 到 1 跳 1 步, 然后跳 3 步到达最后一个位置。

示例 2:

输入: [3,2,1,0,4]
输出: false
解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

 

解题思路：从后往前遍历，当发现当前位置能到达最后一个位置时，把最后一个位置更新为当前位置。

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int r = nums.size() - 1;
        for(int i=r-1; i>=0; i--)
        {
            if(nums[i] >= r-i)
            {
                r = i;
            }
        }
        if(r <= 0)
        {
            return true;
        }
        else
        {
            return false;
        }
    }
};