图的割点问题

#include <stdio.h>
#include<stdlib.h> 
#include <cstring>
#include <iostream>
#include <string.h>
#include <sstream>
#include <math.h>

using namespace std;
int n,m,index,root;
bool vis[105];
int num[105],low[105];
int e[15][15];
void dfs(int cur,int father){                   //cur 此时节点   father 父节点 
    int child=0,i,j;                            //每次搜索 初始化孩子节点数为0 
    index++;                                         //每次深搜时间戳加一 
    num[cur]=index;
    low[cur]=index;                                  //初始化设置该点的num 和low数组 
    for(int i=1;i<=n;i++){
        if(e[cur][i]!=0){                            //生成树过程 cur作为父节点 i作为子节点 节点之间必须相连 
            if(num[i]==0){                            //如果子节点的时间戳为0 表示该节点未被访问过 
                child++;
                dfs(i,cur);                           //继续生成树 
                low[cur]=min(low[cur],low[i]);     //通过子节点更新 该节点可以到达的最小时间戳 
                if(low[i]>=num[cur]&&cur!=root){   //不为根节点的割点条件  low[i]>=num[cur]
                    vis[cur]=1;
                }
                if(cur==root&&child==2){           //根节点的割点条件    child==2
                    vis[cur]=1;
                }
            }
            else if(i!=father){                       //子节点已经被访问过 直接更新该点可以到的最小时间戳 相当于回溯找除父节点之外可到最小时间戳 
                low[cur]=min(low[cur],num[i]);
            }
        }
    }
}
int main ()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            e[i][j]=0;
        }
    }
    int x,y,v;
    for(int i=0;i<m;i++){
        cin>>x>>y;
        e[x][y]=1;
        e[y][x]=1;
    }
    root=1;
    dfs(1,root);
    for(int i=1;i<=n;i++){
        if(vis[i]){
            cout<<i<<endl;
        }
    }
    return 0;
}

首先，什么是割点？

割点就是图中的一个点，不经过这个点图就不连通了，那么这个点就是割点。如下图2这个点就是割点：

然后怎么找图的割点呢？

我们用深搜生成一颗树（不一定是最小生成树），然后用num数组记录生成这颗树过程中每个节点的时间戳(时间戳就是被访问的顺序，一般时间戳不会有相同),

用low数组记录每个节点不经过父节点可以到达的最小时间戳的祖先节点。

 

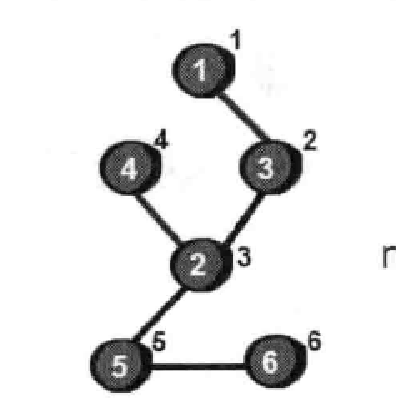
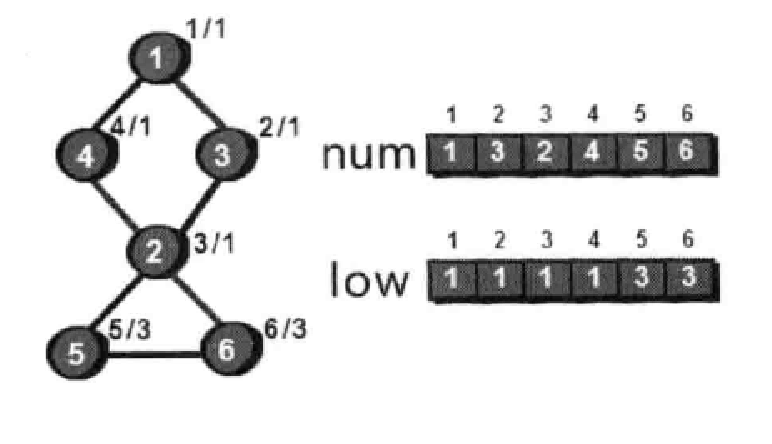
此时有一个结论：

有一个节点father，至少存在一个节点cur，有low[cur]>=num[father] (其中father是父节点，cur是father的子节点)，那么father就是割点。

如果father是根节点时，除了low[cur]>=num[father]还必须father必须至少有两个孩子节点，father才是割点。

输入样例：

6 7
1 2
1 3
1 4
2 5
3 5
4 5
5 6

输出样例：

5

输入样例：

6 7
1 4
1 3
4 2
3 2
2 5
2 6
5 6

输出样例：

2