卷积的理解:
1. 卷积的定义:

对这个表达式,积分变量是τ,f(τ)是输入函数,g(x-τ)是系统响应。设横坐标取x是某个点,其表示的实际含义是求x左边无穷距离到x右边无穷距离输入函数乘以对应权重的积分。
离散化形式:
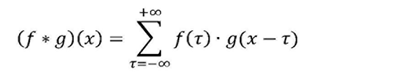
相当于对连续函数取一个个离散的点。
例子:试想小明有一段时间每天都要去输液,输的药会在身体里残留直至失效,药效随着时间是不断衰落的。现在要求某天体内的总药效。(设每天输液后直接增加的药效是10)
药效函数如图:

第一天:小明输液后体内药效增加到10.
第二天:小明前一天的药效是10*0.8,当天又增加药效10,总药效18.
第三天:小明第一天残留药效10*0.6,第二天残留药效10*0.8,当天增加药效10
第三天总药效24.
第四天:第一天药效降为10*0.4,第二天药效降为10*0.6,第三天药效10*0.8,又增加药效10,总药效28.
依此类推……
这里设f(x)为每天增加药效,g(x)设为药效函数,那么某天t身体内总药效可以用卷积公式表达为: 
2.二维卷积公式:
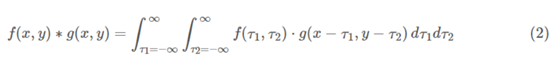
离散形式:
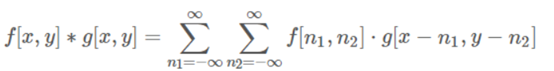
3.二维离散卷积的一个应用:
如求均值滤波:

卷积核运动到(4,4)时
