频域滤波：
(前提)二维傅里叶变化卷积性质：
f(x,y)是空间域信号，F(u,v)是频域信号
h(x,y)是系统冲击函数，H(u,v)是冲击函数频域形式。有:
f(x,y)*h(x,y)=F(u,v)×H(u,v) f(x,y)×h(x,y)=F(u,v)*H(u,v)
空间域卷积对应频域乘积， 空间域乘积对应频域卷积
一．频率滤波原理:
通过滤波系统修正输入图像频率成分，达到图像增强的目的。
利用傅里叶变换的卷积性质，使空间域卷积运算转化为频域乘积运算，有利于对图像进行操作。
频域滤波的基本步骤：
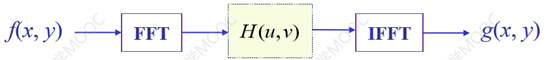
二．频域滤波分为低通滤波器，高通滤波器等。
低通滤波器：（允许低频成分通过，去除高频成分），包括理想低通滤波器，Butterworth低通滤波器，高斯低通滤波器。
我们定义D(u,v)为点(u,v)到原点的距离：D(u,v)=(u²+v²)1/2
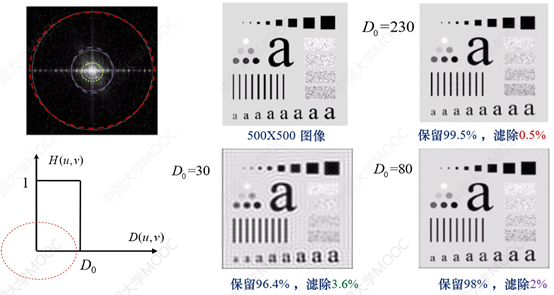
1.理想低通滤波器：H(u,v)满足为
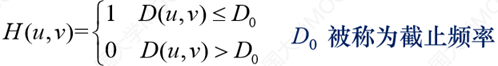
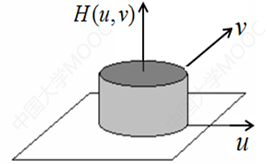
半径为D0圆内的频率成分可以无失真通过；在此半径之外的频率成分被截止（衰减为0）
滤波效果：
2.Butterworth低通滤波器，H(u,v)满足：
（n为阶数）
滤波效果：
3.高斯低通滤波器，H(u,v)满足：
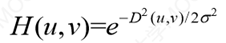（D0为截至频率，D0=σ）
效果：
区别：高斯低通滤波器不能达到相同截止频率的Butterworth低通滤波器平滑效果，高斯低通滤波器没有振铃现象。
低通高斯滤波器的应用：图片文字中字符失真，断符修复。
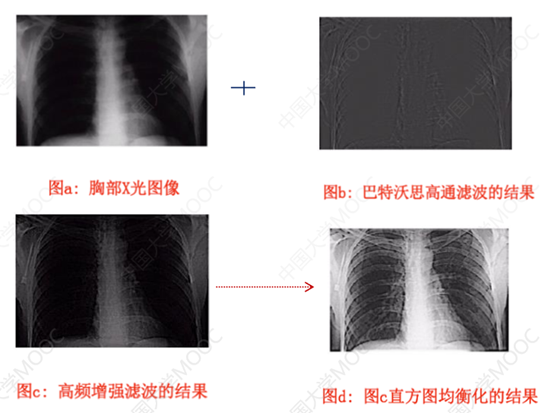
高通滤波器：（高频成分允许通过，抑制低频成分），包括理想高通滤波器，Butterworth高通滤波器，高斯高通滤波器
1.理想高通滤波器：H(u,v)满足:
半径为D0圆外的频率成分可以无失真通过；在此半径之内的频率成分被截止（衰减为0）
效果：
2.Butterworth高通滤波器，H(u,v)满足：
效果：
3.高斯高通滤波器，H(u,v):
（D0为截至频率，D0=σ）
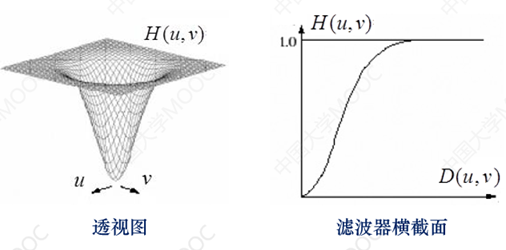
效果
高通滤波器应用：
