Pie or die

题目链接

CF55C

题目

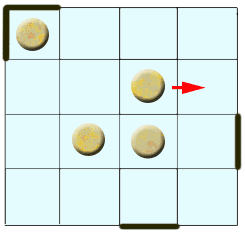
Volodya and Vlad play the following game. There are k pies at the cells of n  ×  m board. Each turn Volodya moves one pie to the neighbouring (by side) cell. If the pie lies at the border of the board then Volodya can move it outside the board, get the pie and win. After Volodya's move, Vlad bans some edge at the border of the board of length 1 (between two knots of the board) so that Volodya is not able to move the pie outside the board through this edge anymore. The question is: will Volodya win this game? We suppose both players follow the optimal strategy.

n*m的棋盘，k个pie，Volodya是先手，他可以移动pie上下左右，如果有pie移除棋盘，Volodya赢。Vlad是后手，可以堵住一个边界。问你谁赢。

思路

• 日常不会博弈题 别人的水题 我的难题
• 我的思路：好像是与四个角有关，如果角堵上了，就没办法把pie移出去了
• 我以为要把所有的pie都移出去才算赢....
• 别人的思路：如果能在四个角都堵上一边，那么Vlad就可以赢了。
• 怎么在四个角都堵一条边呢？那就是在pie移到最近的边界的时候Vlad去堵四个角，所以如果这个pie的位置与最近的边界相隔4及以下个格子，那么Volodya会赢。
• 注意坐标x,y和n,m和格子之间的关系。

代码

#include<bits/stdc++.h>
using namespace std;
int main(){
	int n,m,k;
	scanf("%d%d%d",&n,&m,&k);
	bool flag=false;
	int x,y;
	while(k--){
		scanf("%d%d",&x,&y);
		x=x>n-x?n-x+1:x;
		y=y>m-y?m-y+1:y;
		if(min(x,y)<=5){
			flag=true;
			break;
		}
	}
	printf(flag?"YES
":"NO
");
	return 0;
}