“科林明伦杯”哈尔滨理工大学第十届程序设计竞赛 部份签到题

直线

题意

平面上存在n条直线。请问n条直线在平面上最多存在多少交点。

思路

• (a[i] = a[i-1] + i-1; a[1]=0)
• (a[i] = frac{n*(n-1)}{2})
• wa 了一次 在python的 // 写成了 /

代码

t = input()
t = int(t)
while t:
    n = input()
    n = int(n)
    print(n*(n-1)//2)
    t = t-1

减成一 贪心

题意

存在n个数，每次操作可以任选一个区间使得区间内的所有数字减一。问最少多少次操作，可以让所有数都变成1。
数据保证一定有解。

思路

• 我的思路：把所有值-1 然后 极大值之和-极小值之和
  • 注意第一个点和最后一个点，如果第一个点和最后一个点是极小值，那么久不用减去它，如果是极大值则要加上
  • 因为极小值的部份可以让左右两遍一起，这个大区间一起减。
    
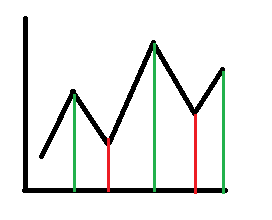
• 有人说 差分，于是我去搜了下差分
  • 差分：相邻两个数的差
  • (p_i = a_i - a_{i-1}) p为a的差分数组
  • 便于整个区间 加减
  • 例如在[l, r]加k， 则 (p[l]+=k, p[r+1]-=k), 注意是r+1。
    

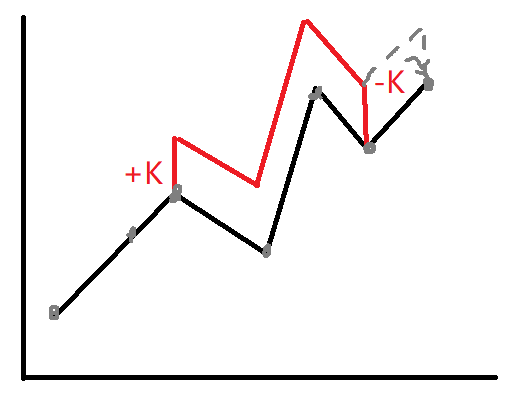
代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN= 100005;
int a[MAXN];
int main()
{
    int n,T;
    scanf("%d",&T);
    while(T--){
        scanf("%d",&n);
        if(n==0){
            printf("%d
",0);continue;
        }
        int sumh=0,suml=0;
        bool flag=false;
        scanf("%d",&a[1]);
        a[1]--;
        if(n==1){
            printf("%d
",a[1]);
            continue;
        }
        for(int i=2;i<=n;i++){
            scanf("%d",&a[i]);
            a[i]--;
            if(a[i]<a[i-1]&&!flag){
                flag=true;
                sumh+=a[i-1];
            }
            else if(a[i]>a[i-1]&&flag){
                flag=false;
                suml+=a[i-1];
            }
        }
        if(!flag){
            sumh+=a[n];
        }
        printf("%d
",sumh-suml);
    }
}

最大值 next数组 字符串

题意

有一个字符串s，对于字符串中一个非前缀子串恰好为字符串的前缀我们称之为ac串。
请问给出一个字符串他的ac串最大长度为多少

思路

• 就是求next数组的最大值
• next[i]: x[i-z...i-1] = x[0...z-1] 的最大z值
• 注意要初始化next的值为-1，还要注意m值 ，没初始化wa了一次
• next这个名字不知道为什么交的时候会有问题

代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN =100005;
char s[MAXN];
int nxt[MAXN];
void kmp_pre(char x[],int m){
    int i,j;
    j = nxt[0] = -1;
    i = 0;
    while(i<=m){
        while(j!=-1 && x[i]!=x[j]) j=nxt[j];
        nxt[++i] = ++j;
    }
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%s",&s);
        memset(nxt, -1 ,sizeof(nxt));
        int len = strlen(s);
        kmp_pre(s,len);
        int mx=0;
        for(int i=0;i<=len;i++){
            mx=nxt[i]>mx?nxt[i]:mx;
        }
        printf("%d
",mx);
    }
    return 0;
}

三角形 打表

题意

小明有一根长度为a的木棒，现在小明想将木棒分为多段（每段木棒长度必须为整数），
使得分隔后的木棍中，取出的任意三段都不能构成三角形，小明想知道木棒最多被分成几段？

思路

• 如果a,b,c 其中a最小，c最大，能构成三角形则 (a+b>c)
• 因此，a,b,c,其中a最小，c最大, 不能构成三角形则 (a+b<=c)
• 注意a+b==c也是不能构成的！！！！wa了足足3次！
• 可以推出 (a[i] = a[i-1] + a[i-2]) a[i]: 从小到大第i个可以的长度
• 用tot数组存前i个长度之和
• 因此只用在tot数组里面找lower_bound就好了，但是我用python写，二分写的有问题，然后输出所有在范围里的tot值，根本就没几个，直接暴力一个个查了。
• 可能的长度，从小到大前几个有: 1 1 2 3 5 8 13....

代码

T = input()
T = int(T)
a = 1
b = 1
dic = []
tot = 2
dic.append(1)
dic.append(2)
c = 0
 
while True:
    if tot > (1 << 65):
        break
    c = a + b
    tot += c
    dic.append(tot)
    a = b
    b = c
while T:
    T = T - 1
    x = input()
    x = int(x)
    left = 0
    r = len(dic) - 1
    mid = 0
    for mid in range(0, len(dic)):
        if dic[mid] > x:
            mid -= 1
            break
    print(mid + 1)