Merge Sort

Merge Sort 的递归实现， 同时也是算法里面常见的分而治之方法。

先放上一段分而治之的算法定义, 一张图胜过千言万语。

 

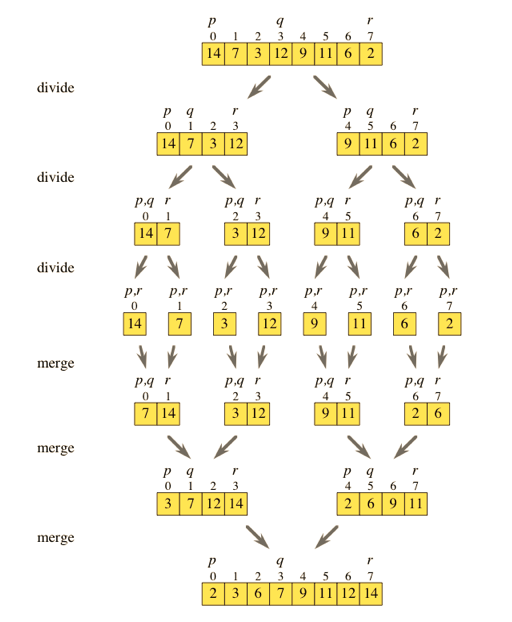
1. sort 整个数组 = sort 前半个数组， then sort后半个数组， then merge两个有序数组。
2. merge整个有序数组是非递归程序，输入有array本身，left， middle 和 right
   1. 左半数组长度，有半数组长度
   2. 初始化两个新数组
   3. 两个新数组比较，比较结果更新到原来的数组里
   4. 比较完以后，有一个数组可能有碎片，将碎片加到原数组中

 下面是实现代码：

    public class MergeSortV1
    {
        public void PrintArray(int[] array)
        {
            for (int i = 0; i < array.Length; i++)
            {
                Console.WriteLine(array[i]);
            }
        }

        public void Sort(int[] array, int left, int right)
        {
            if (left < right)
            {
                int middle = (right + left) / 2;
                Sort(array, left, middle);
                Sort(array, middle + 1, right);
                Merge(array, left, middle, right);
            }
        }

        public void Merge(int[] array, int left, int middle, int right)
        {
            int n1 = middle - left + 1;
            int n2 = right - middle;

            int[] L = new int[n1];
            int[] R = new int[n2];

            for(int i = 0; i < n1; i++)
            {
                L[i] = array[middle - left + i];
            }

            for(int i = 0; i < n2; i++)
            {
                R[i] = array[right - middle + i];
            }

            // merge two sorted array to one
            int leftIndex = 0, rightIndex = 0;
            int k = left;
            for(leftIndex = 0; leftIndex < n1; leftIndex++)
            {
                while(rightIndex < n2)
                {
                    if (L[leftIndex] < R[rightIndex])
                    {
                        array[k] = L[leftIndex];
                        k++;
                        break;
                    }
                    else
                    {
                        array[k] = R[rightIndex];
                        k++;
                        rightIndex++;
                    }
                }

                if (rightIndex == n2 - 1)
                {
                    break;
                }
            }

            // assign the remaining part
            while(leftIndex < n1)
            {
                array[k++] = L[leftIndex++];
            }

            while (rightIndex < n2)
            {
                array[k++] = R[rightIndex++];
            }
        }
    }