本博客在在这里重新总结了一下,当前常用的经典数据结构;这里只针对链表,顺序表,简单树和图进行总结;具体实现请参考:https://github.com/yaowenxu/codes/tree/master/数据结构; 本文章,主要讨论数据结构的性质;以及对这些数据结构的性质;主要是用来知识整理与复习;
顺序表:顺序表是指,将元素顺序地存放在一块连续的内存中;元素间的顺序关系由他们的存储顺序自然表示;c++声明一个数组:int a[10]; 即构建了10个int内存大小(40bytes)的顺序表;
优点:顺序存储,O(1)的时间进行访问;
缺点:当容量不够用时,需要重新构建结构,产生大量内存拷贝;删除和插入数据时,数据移动开销较大;

链表:链表相对于顺序表可以充分利用计算机内存空间;顺序表是内存上连续的一块位置,其在构建时需要预先知道数据大小来申请连续的内存空间;而在顺序表进行扩充的时候,需要对顺序表进行拷贝迁移,并释放旧空间,产生较多的内存拷贝;而链表可以在空间不足的时候,可以直接声明节点并分配内存,放到链表的末尾;这样可以方便实现内存的灵活管理;(注意:在实现插入和删除节点的时候,可以先在本子上把过程画出来,再来使用代码实现)
优点:节省内存,动态管理内存;在删除和增加数据的时候为O(1),没有顺序表的复制和拷贝的开销;
缺点:只能顺序访问,不能随机访问;同时增加了节点指针索引,所以控销开销较大;
单向链表:node之中只有 next索引; 链表中最简单的一种形式,是一种线性表,不像顺序表一样连续存储数据,而是每个节点中存放下一个节点的位置信息,最后一个节点为空指针;

双向链表:每个节点有 next和prev指针,用于指向前一个节点和后一个节点;其中第一个节点prev指针为空,最后一个节点next指针为空;
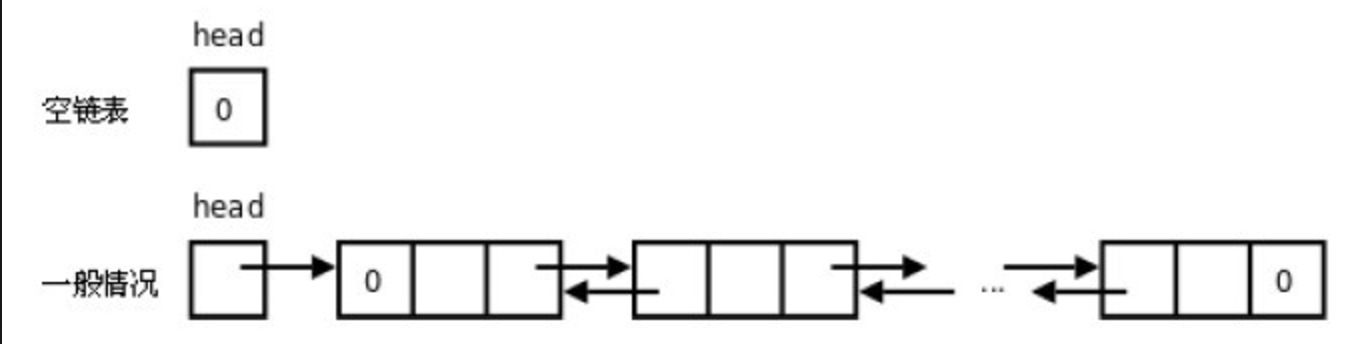
单向循环链表:单链表的一个变形,指链表的最后一个节点的next 不再是空,而是指向头结点;头结点由head指针进行标识,为单向链表的第一个节点;

栈:为一种常用的经典数据结构,其只能在一端进行操作push 和 pop, 遵循先入先出规则(LIFO, Last In First Out);栈可以使用顺序表和链表模拟实现;
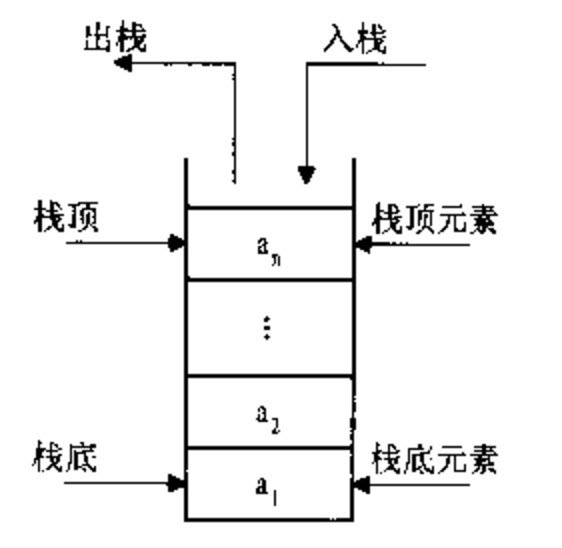
队列:为一种常用的经典数据结构,其允许在一端进行插入,另外一端进行删除操作;遵循先进先出策略(First In First Out);可以使用瞬息表和链表模拟实现;

双端队列(deque):全名为double-ended queue, 可以模拟队列和栈的操作;双端队列中的元素可以从两端弹出;插入只可以在两端插入,双端队列可以在队列的任意一端进行出队和入队操作;

队列变种:优先队列(priority queue),队列中每个元素具有优先级,新的队列进行入队时,会根据优先级进行重新排序,重新定位到特定的位置;优先队列方便使用链表进行实现;
树:树的经典结构为二叉树结构;它是又有限节点组成的一个具有层次关系的集合。树有如下特点:
- 每个节点有零个或者多个子节点;
- 没有父节点的点为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点以外,每个节点可以分为多个不相交的子树;
树的属性:
- 节点的度:该节点子节点的个数;
- 树的度:一颗树中,最大的节点的度,为树的度;
- 根节点:没有父节点的节点;
- 叶节点:度为零的节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 节点层次:从根开始定义起,根为第一层,根的子节点为第二层;以此类推;
- 树的高度或深度:节点最大层次;
- 堂兄弟节点:父节点在同一层的节点为堂兄弟;
- 节点的祖先:从根到节点所经分支上的所有节点;
- 子孙:以某以节点为根的子树中任一节点都称为该节点的子孙;
树的种类:
- 无序树:树中任意节点之间没有顺序关系,这种树为无序树,也称为自由树;
- 有序树:树中任意节点的子节点之间有顺序关系为有序树;
- 二叉树:每个节点最多含有两个子树的树,称之为二叉树(节点度<=2);
- 完全二叉树:对于一颗二叉树,其深度为d(d>1)。除d层以外,其他各层的节点数目均已达到最大值;第d层所有节点从左到右连续地紧密排列,这样的二叉树称为完全二叉树,其中满二叉树的定义是最底层的所有叶节点都在的完全二叉树;
- 平衡二叉树:当且仅当任何节点的两棵子树的高度差不大于1的二叉树;
- 排序二叉树(二叉查找树,binary searcg tree):
- 若左子树不空,则左子树上所有节点的值都小于它的根节点的值;
- 若右子树不空,则右子树上所有节点的值都大于它的根节点的值;
- 左右子树也分别为二叉排序树;
- 没有键值相等的节点;
树的存储与表示:
- 顺序表存储:完全二叉树可以用一个数组来进行表示,对于一个节点索引为i; 其父节点索引为 (n-1)/2; 其左孩子节点为 2i+1; 右孩子节点为2i+2; (堆排序使用此种方法实现;)
- 链式存储:对于一个节点,其包含了两个指针,left 和 right分别指向左孩子和右孩子;常用此种方法实现树结构;
树的遍历:二叉树遍历算法的实现请参考:https://github.com/yaowenxu/codes/blob/master/数据结构/二叉树.cc
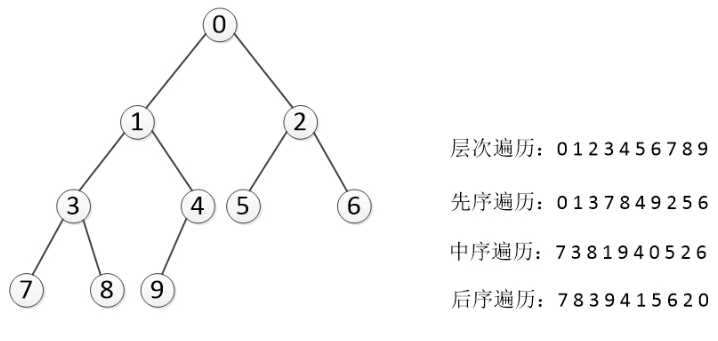
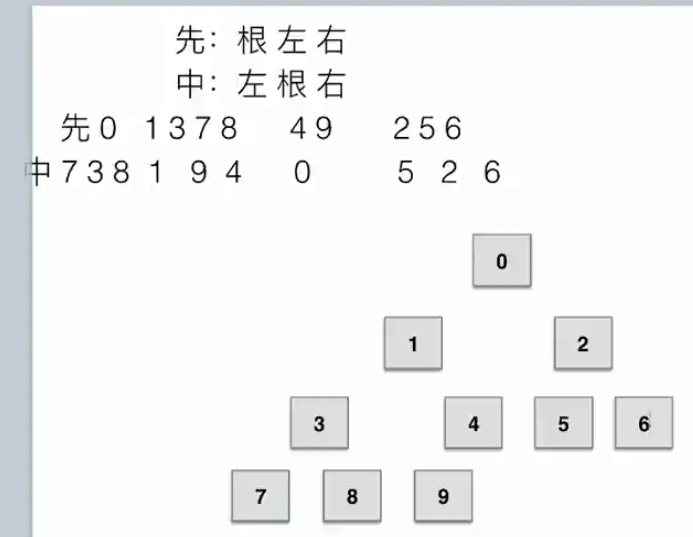
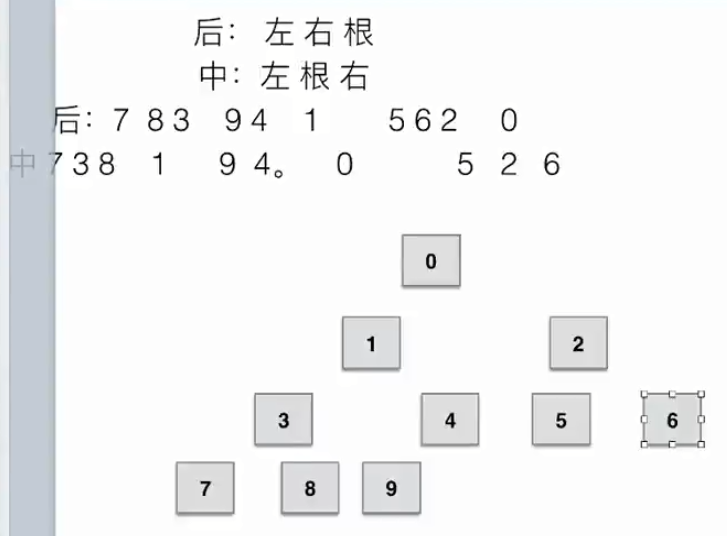
- 深度优先遍历(Depth First Search):沿着树的深度遍历树的节点,尽可能深得搜索树的分支,根据根节点的访问次序不同,又细分为三种:
- 先序遍历:根节点-左子树-右子树
- 中序遍历:左子树-根节点-右子树
- 后续遍历:左子树-右子树-根节点
- 先序遍历,中序遍历和后序遍历给两种遍历就可以推出树,但是这两种遍历一定要包含中序遍历;
- 只要给出先序就可以判断出所有根,通过各段首元素查看根,第一个元素肯定是整棵树的根。
- 只要给出后序就可以判断出所有根,通过各段末元素查看根,最后一个元素肯定是整棵树的根。
- 广度优先遍历(Breadth First Search): 从树的根开始,从上到下,从左到右遍历整个树的节点;
- 深度优先遍历一般用递归实现,广度优先一般使用队列实现;一般情况下能用递归实现的大部分算法也能用堆栈来进行实现;
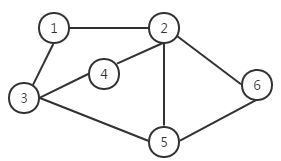
图结构:图G由顶点V和边E构成;边可以是单向的和双向的;权重可以加在边和顶点上;图有有向图和无向图;一个顶点有出度和入度;实际生活中的交通运输网,社交网络都可以利用图来进行表示;
无向图与有向图:
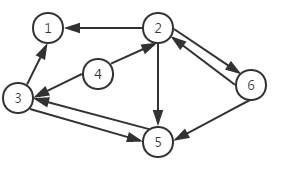
无向完全图:每两个点之间,都存在边;

有向完全图:每两个点之间,都存在相反的两条边;
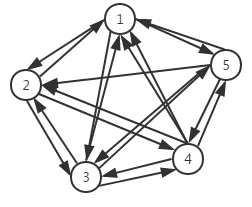
有向无环图:如果一个有向图无法从某个顶点出发经过若干条边回到该点,则这个图是一个有向无环图。
无权与有权图;图的连通性;
简单图:不考虑平行边和自环边的图;
图的表示:
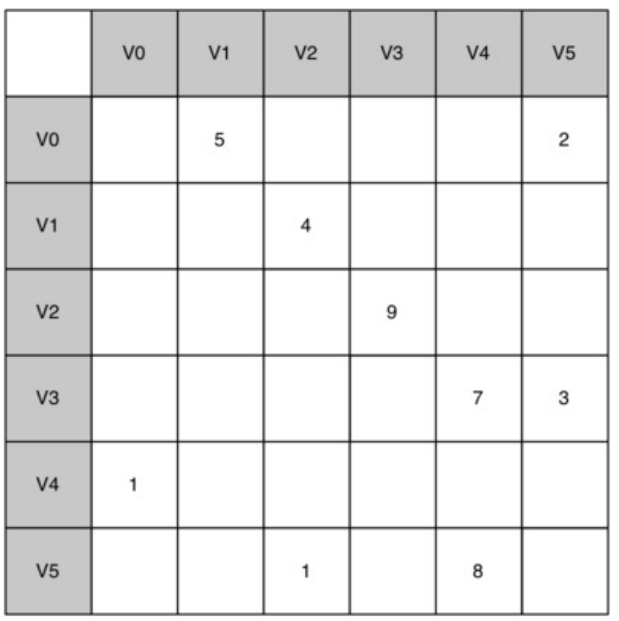
邻接矩阵:v表示顶点,表中的数组表示权重;
邻接表:在邻接表中,我们保存所有节点的主列表;每个顶点维护一个链接到其他节点的列表和权重;对于 每个顶点维护的列表可以使用map 来进行实现;

至此,经典的数据结构基本概括完毕;后续运用过程中,会继续进行补充;
保持更新,转载请注明出处;更多内容请关注cnblogs.com/xuyaowen;
参考博客:注:文中图片整理自参考博客;