一. 时间复杂度
#在计算机科学中,算法的时间复杂度是一个函数,它定性描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。 时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。 #时间复杂度是用来估计算法运行时间的一个式子(单位) #如何一眼判断时间复杂度? - 循环减半的过程->O(logn) - 几次循环就是n的几次方的复杂度
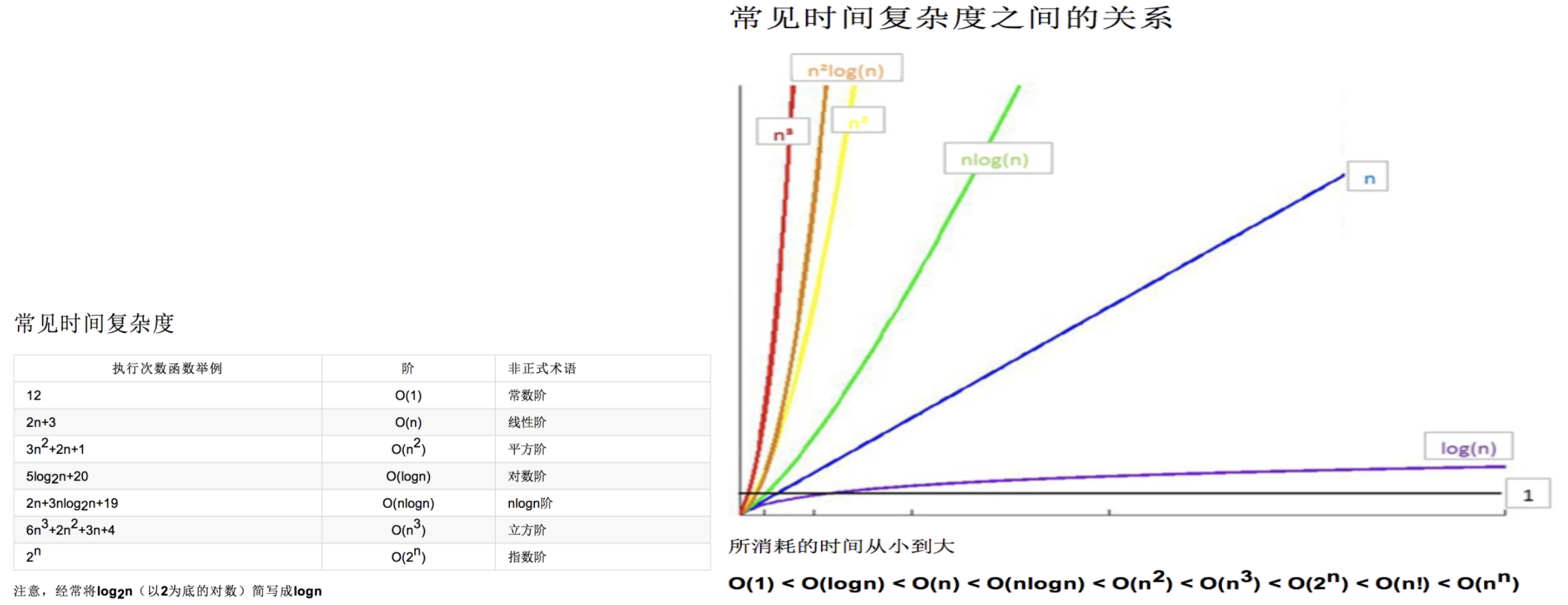
#时间复杂度 - 最优时间复杂度 - 最坏时间复杂度 - 平均时间复杂度 #时间复杂度的几条计算规则 - 基本操作 即只有常数项,认为其时间复杂度为O(1) - 顺序结构 时间复杂度按加法进行计算 - 循环结构 时间复杂度按乘法进行计算 - 分支结构 时间复杂度取最大值 - 判断一个算法的效率时, 往往只需要关注操作数量的最高次项, 其它次要项和常数项可以忽略 - 在没有特殊说明时,我们分析的算法的时间复杂度都是指最坏时间复杂度
a. 测试

# coding:utf-8 from timeit import Timer # li1 = [1, 2] # # li2 = [23,5] # # li = li1+li2 # # li = [i for i in range(10000)] # # li = list(range(10000)) def t1(): li = [] for i in range(10000): li.append(i) def t2(): li = [] for i in range(10000): li += [i] def t3(): li = [i for i in range(10000)] def t4(): li = list(range(10000)) def t5(): li = [] for i in range(10000): li.extend([i]) timer1 = Timer("t1()", "from __main__ import t1") print("append:", timer1.timeit(1000)) timer2 = Timer("t2()", "from __main__ import t2") print("+:", timer2.timeit(1000)) timer3 = Timer("t3()", "from __main__ import t3") print("[i for i in range]:", timer3.timeit(1000)) timer4 = Timer("t4()", "from __main__ import t4") print("list(range()):", timer4.timeit(1000)) timer5 = Timer("t5()", "from __main__ import t5") print("extend:", timer5.timeit(1000)) def t6(): li = [] for i in range(10000): li.append(i) def t7(): li = [] for i in range(10000): li.insert(0, i) #------------------结果------- append: 1.0916136799496599 +: 1.0893132810015231 [i for i in range]: 0.4821193260140717 list(range()): 0.2702883669990115 extend: 1.576017125044018

def t6(): li = [] for i in range(10000): li.append(i) def t7(): li = [] for i in range(10000): li.insert(0, i) timer6 = Timer("t6()", "from __main__ import t6") print("append", timer6.timeit(1000)) timer7 = Timer("t7()", "from __main__ import t7") print("insert(0)", timer7.timeit(1000)) #################### append 1.1599015080137178 insert(0) 23.26370093098376
b. 二分法

import random n = 10000 li = list(range(n)) def bin_search(li,val): low = 0 high = len(li) - 1 while low <= high: mid = (low + high) // 2 if li[mid] == val: return mid elif li[mid] < val: low = mid + 1 else: high = mid - 1 return None obj = bin_search(li,5550) print(obj)
题一:已知列表li=[5,7,7,8,8,10] 和 target = 8,求列表二个不同索引的value值相加为target,并且算法复杂度为O(log n).
即:li[a]+li[b]=target,返回索引值

def bin_search(data_set,val): low = 0 high = len(data_set) - 1 while low <= high: mid = (low+high)//2 if data_set[mid] == val: a = mid b = mid while data_set[a] == val and a>0: a -= 1 while data_set[b] == val and b<len(data_set): b += 1 return (a+1,b-1) elif data_set[mid] > val: high = mid - 1 else: low = mid + 1 return None
题二: 已知列表li=[2, 7, 11, 15],target=9, li[i]+li[j]=target,索引i不等于j. 求i,j

法一: def two_sum(li, target): l = len(li) for i in range(l): for j in range(i+1, l): if li[i] + li[j] == target: return (i, j) return None print(two_sum([2, 7, 11, 15], 17)) 法二: 二分查找 def bin_search(data_set, value): low = 0 high = len(data_set) - 1 while low <= high: mid = (low + high) // 2 if data_set[mid] == value: return mid elif data_set[mid] > value: high = mid - 1 else: low = mid + 1 def two_sum_2(li, target): li.sort() for i in range(len(li)): b = target - li[i] j = bin_search(li, b) if j != None and i != j: return i, j print(two_sum_2([2, 7, 11], 14)) 法三: def two_sum_3(li, target): li.sort() i = 0 j = len(li) - 1 while i<j: sum = li[i]+li[j] if sum > target: j-=1 elif sum < target: i+=1 else: #sum==target return (i,j) return None
c. 排序
#排序low B三人组 - 冒泡排序
比较相邻的元素。如果第一个比第二个大,就交换他们两个。依次进行排序。
- 选择排序
一趟遍历记录最小的数,放到第一个位置。再一趟遍历剩余
- 插入排序
摸牌插入,将牌从无序区放到手中有序区,最开始手中有序区只有一张,后面抽牌放入手中有序区。
#快速排序
取第一个位置的数,剩下列表中左右元素分别与取出的数比较,如果数比取出的数小,则放到列表的左边;如果数比取出的数大,则放到列表的右边。 #排序NB二人组 - 堆排序 - 归并排序 #么人用的排序 - 基数排序 - 希尔排序 - 桶排序

#冒泡排序 - 列表每相邻的数,如果前边的比后边的大,那么交换这两个数 - 算法复杂度 n^2 import random def bubble_sort(li): for i in range(len(li) - 1): # i 趟 for j in range(len(li) - i -1): # j 指针 if li[j] > li[j+1]: li[j],li[j+1] = li[j+1],li[j] return li li = list(range(10)) random.shuffle(li) obj = bubble_sort(li) print(obj)

# 选择排序 - 一趟遍历记录最小的数,放到第一个位置;再一趟遍历记录剩余列表中最小的数,继续放置... - 时间复杂度 O(n^2) def select_sort(li): for i in range(len(li) - 1): #i 趟 min_loc = i # 找i+1位置到最后面位置内最小的数 for j in range(i+1,len(li)): if li[j] < li[min_loc]: min_loc = j # 和无序区第一个数作交换 li[min_loc],li[i] = li[i],li[min_loc] return li obj = select_sort([1,8,6,2,5,3]) print(obj)

#插入排序 - 列表被分为有序区和无序区 最初有序区只有一个元素 - 每次从无序区选择一个元素 插入到有序区的位置 直到无序区变空 #方式一: def insert_sort(li): for i in range(1,len(li)): # i 代表每次摸到牌的下标 tmp = li[i] j = i-1 # j代表手里最后一张牌的下标 while True: if j<0 or tmp>=li[j]: break li[j+1] = li[j] j -= 1 li[j+1] = tmp return li obj = insert_sort([1,8,6,2,5,3]) print(obj) #方式二: def insert_sort(li): for i in range(1,len(li)): # i 代表每次摸到牌的下标 tmp = li[i] j = i-1 # j代表手里最后一张牌的下标 while j>=0 and tmp<li[j]: li[j+1] = li[j] j -= 1 li[j+1] = tmp return li obj = insert_sort([1,8,6,2,5,3]) print(obj)

def partition(data,left,right): tmp = data[left] while left < right: # right 左移动 while left < right and data[right] >= tmp: #如果low和high没有相遇且后面的数一直大于第一个数 就循环 right -=1 data[left] = data[right] # left 右移动 while left < right and data[left] <= tmp: #如果low和high没有相遇且后面的数一直大于第一个数 就循环 left +=1 data[right] = data[left] data[left] = tmp return left def quick_sork(data,left,right): if left <right: mid = partition(data,left,right) quick_sork(data,left,mid-1) quick_sork(data,mid+1,right) return data alist = [33,22,11,55,33,666,55,44,33,22,980] obj = quick_sork(alist,0,len(alist)-1) print(obj)

def shift(data,low,high): # shift函数复杂度:O(logn) """ 调整函数 data: 列表 low:待调整的子树的根位置 high:待调整的子树的最后一个节点的位置 """ i = low # i指向空位置 j = 2*i + 1 tmp = data[low] while j<=high: #领导已经撸到底了 if j != high data[j] < data[j+1] j+=1 #j指向数值大的孩子 if tmp<data[j]: #如果小领导比撸下来的大领导能力值大 data[i] = data[j] i = j j = 2*i+1 else: #撸下来的领导比候选的领导能力值大 data[i] = tmp break else: data[i] = tmp @cal_time def heap_sort(data): # heap_sort函数复杂度:O(nlogn) n = len(data) # 建堆 for i in range(n//2-1,-1,-1): shift(data,i,n-1) # 挨个出数 for high in range(n-1,-1,-1): data[0],data[high] = data[high],data[0] shift(data,0,high-1)

# 一次归并 def merge(li,low,mid,high): i = lowe j = mid+1 ltmp = [] while i <= mid and j <= high: if li[i] <= li[j]: ltmp.append(li[i]) i +=1 else: ltmp.append(li[j]) j +=1 while i<=mid: ltmp.append(li[i]) i += 1 while j<=high: ltmp.append(li[j]) j += 1 li[low:high+1] = ltmp def mergesort(li,low,high): if low<high: mid = (low+high)//2 mergesort(li,low,mid) mergesort(li,mid+1,high) merge(li,low,mid,high)
总结: 三种排序算法的时间复杂度都是O(nlogn) 运行时间:快速排序 < 归并排序 < 堆排序 三种排序算法的缺点: 快速排序:极端情况下排序效率低 归并排序:需要额外的内存开销 堆排序:在快的排序算法中相对较慢
二叉树递归遍历

class Node(): def __init__(self, data, left, right): self.data = data self.left = left self.right = right

class BTree: def __init__(self): self.root = None def insert(self, data): #插入节点 r = self.root if r is None: self.root = Node(data, None, None) return while True: # 比根结点小放在左边 if r.data > data: if r.left is None: r.left = Node(data, None, None) break else: r = r.left else: # 比根结点大放在右边 if r.right is None: r.right = Node(data, None, None) break else: r = r.right

def preoder(self, root): if root is None: return else: print root.data self.preoder(root.left) self.preoder(root.right)

def midoder(self, root): if root is None: return else: self.midoder(root.left) print root.data self.midoder(root.right)

def postoder(self, root): if root is None: return else: self.postoder(root.left) self.postoder(root.right) print root.data

if __name__ == '__main__': bt = BTree() L=[3,7,5,8,9,10,11,2,6,4] for i in L: bt.insert(i) bt.preoder(bt.root) bt.midoder(bt.root) bt.postoder(bt.root)

class Node(): def __init__(self,root): self.root=root self.lchild=None self.rchild=None class Bitree(): def __init__(self): self.root=None def insert(self,root,node): #插入节点 if root: if root.root>node.root: if root.lchild: self.insert(root.lchild,node) else: root.lchild=node else: if root.rchild: self.insert(root.rchild,node) else: root.rchild=node else: return 0 def initBitree(self,data): #生成二叉树 root=Node(data[0]) length=len(data) for x in range(1,length): node=Node(data[x]) self.insert(root,node) return root def preoder(self,root): #先序遍历 if root: print(root.root) self.preoder(root.lchild) self.preoder(root.rchild) def midoder(self,root): #中序遍历 if root: self.midoder(root.lchild) print(root.root) self.midoder(root.rchild) def postoder(self,root): #后序遍历 if root: self.postoder(root.lchild) self.postoder(root.rchild) print(root.root) if __name__ == '__main__': data=[3,7,5,8,9,10,11,2,6,4] Bitree=Bitree() a=Bitree.initBitree(data) print('前序遍历:') Bitree.preoder(a) print('中序遍历:') Bitree.midoder(a) print('后序遍历:') Bitree.postoder(a)
