青蛙跳台阶问题-斐波拉契数列

题目1：一个台阶总共有n级，如果一次可以跳1级，也可以跳2级。求总共有多少种跳法

　　首先我们考虑最简单的情况，加入只有1级台阶，那显然只有一种跳法，如果有2级台阶，那就有两种跳的方法了；一种是分两次跳，每次跳1级；另外一种就是一次跳2级

　　现在我们来讨论一般情况。我们把n级台阶时的跳法看成是n的函数，记为f(n)。当n>2时，第一次跳的时候就有两种不同的选择：一是第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即为f(n-1)；另外一种选择是第一次跳2级，此时跳法数目等于后面剩下的 n-2级台阶的跳法数目，即为f(n-2)。因此n级台阶时的不同跳法的总数f(n) = f(n-1) + f(n-2)

　　把上面的分析过程用一个公式总结：

　　　　/   1　　　　　　　　n=1

　　f(n) =   2　　　　　　　　n=2

　　　　   f(n-1) + f(n-2)           n>2

　　这就是我们的 斐波拉契数列

代码实现：

　　递归式：

int Fib(int n)  {  
　　if (n <= 0)  {    
　　　　return -1;  
　　}  
   
　　if (n<=2 && n > 0)  {  
　　　　return n;  
　　} else  {  
　　　　return Fib(n - 1) + Fib(n - 2);  
　　}  
}

　　非递归式：

long Fib2(long n){
    int f1 =    0;
    int f2 =    1;
    int f3;
    int i;
    for(i=2;i<=n;i++){
        f3 =    f2 + f1;
        f1 =    f2;
        f2 =    f3;
    }
    return f3;

}

题目2：一个台阶总共有n级，如果一次可以跳1级，也可以跳2级......它也可以跳上n级。此时该青蛙跳上一个n级的台阶总共有多少种跳法？

　　分析：用Fib（n）表示青蛙跳上n阶台阶的跳法数，青蛙一次性跳上n阶台阶的跳法数为1，设定Fib（0） =  1，代表一次跳n阶的跳法数为一次

　　当 n =1 时，只有一种跳法，即1阶跳：Fib1（1） = 1

　　当 n = 2时，有两种跳的方法，一阶跳和二阶跳：Fib（2） = Fib（1） + Fib（0） =  2

　　当 n = 3时，有三种跳的方式，第一次跳出一阶后，后面还有Fib(3-1)中跳法； 第一次跳出二阶后，后面还有Fib(3-2)中跳法；第一次跳出三阶后，后面还有Fib(3-3)中跳法

　　Fib(3) = Fib(2) + Fib(1)+Fib(0)=4;

　　当n = n 时，共有n种跳的方式，第一次跳出一阶后，后面还有Fib(n-1)中跳法； 第一次跳出二阶后，后面还有Fib(n-2)中跳法..........................第一次跳出n阶后，后面还有 Fib(n-n)中跳法

　　 Fib(n) = Fib(n-1)+Fib(n-2)+Fib(n-3)+..........+Fib(n-n)=Fib(0)+Fib(1)+Fib(2)+.......+Fib(n-1)

　　又因为当n = n - 1时，Fib(n-1)=Fib(0)+Fib(1)+Fib(2)+.......+Fib(n-2)

　　

　　两式相减  ==》  Fib(n)-Fib(n-1)=Fib(n-1)   ==》Fib(n) = 2*Fib(n-1)     n >= 2

　　最终得到的递归：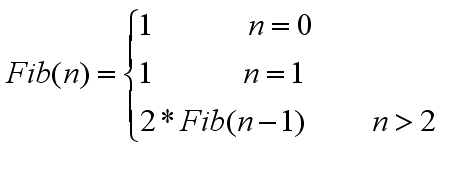

参考：http://www.cnblogs.com/batys/archive/2013/09/19/3329955.html