本博客适合那些BP网络很熟悉的读者
一 基本结构和前向传播
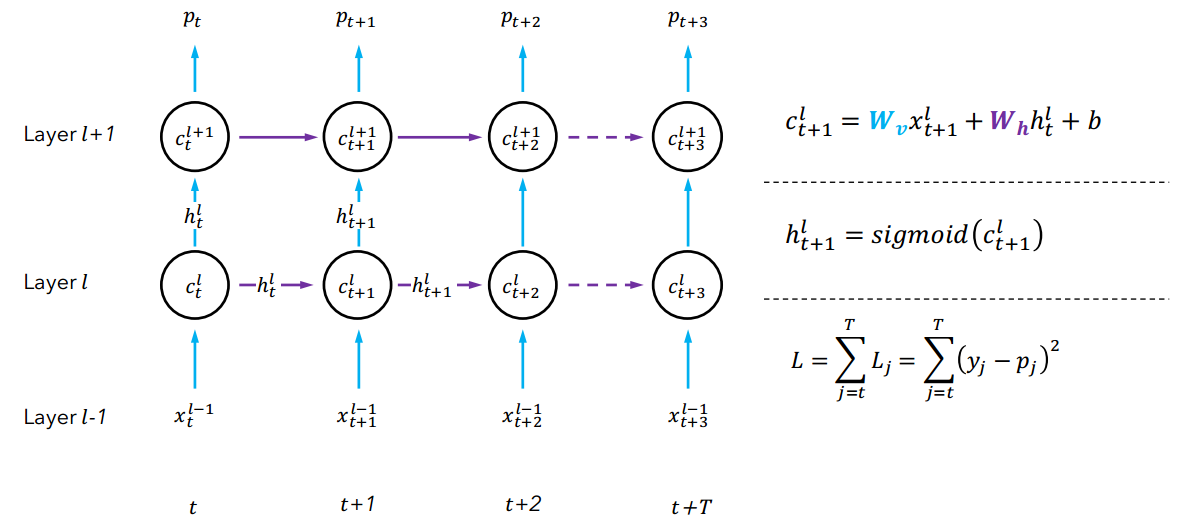
符号解释:
1. $c_{t}^{l}$:t时刻第l层的神经元的集合,因为$c_{t}^{l}$表示的是一层隐藏层,所以图中一个圆圈表示多个神经元。
2. $h_{t}^{l}$:第l层在t时刻的输出。因为$h_{t}^{l}$是一层隐藏层的输出,所以表示的是一个向量。
3. $L_{j}$:表示的是在j时刻,网络的输出的值和目标输出值的平方差,L表示的是所有时刻的平方差的和。
4. $W_{v}$:是一个矩阵,表示的是输入x到c的权值矩阵,那么他的大小是(c的维度)x(x的维度)。
5. $W_{h}$:是一个矩阵,表示的是输入同一层的上一个时刻h到c的权值矩阵,那么他的大小是(c的维度)x(h的维度)。
6. b:表示的是偏置。
(PS:个人感觉c,h和W这些符号表示的维度很重要,因为理解了维度,才能更好的理解网络的结构,才能更好的去实现这个结构。另外在这里我们要学习的参数是$W_{v}$和$W_{h}$)
图中左边的网络结构是一个RNN的时序上展开的结构,所有的列表示的是同一个神经网络,只是时间依次排开而已,紫色(横向)的箭头表示的是时序上的联系。蓝色(竖向)的箭头表示的是空间上的传播(也就是普通的前向传播),而紫色(横向)的箭头表示的上一个时刻隐藏层的输出和当前时刻上一层的输出共同组成当前隐藏层的的输入。例如:$c_{t+1}^{l+1}$表示的是t+1时刻第l+1层,那么这一层的输入是该层的上一个时刻的输出$h_{t}^{l+1}$和当前时刻的上一层的输出$h_{t+1}^{l}$共同作为$c_{t+1}^{l+1}$的输入。
图中右边的公式分别是$c_{t+1}{l}$的输入;$c_{t+1}{l}$的输入的输出,用$h_{t+1}{l}$表示;所有时刻的平方差的和。
二 梯度爆炸或梯度消失
2.1 Back-Propagation Through Time (BPTT)算法
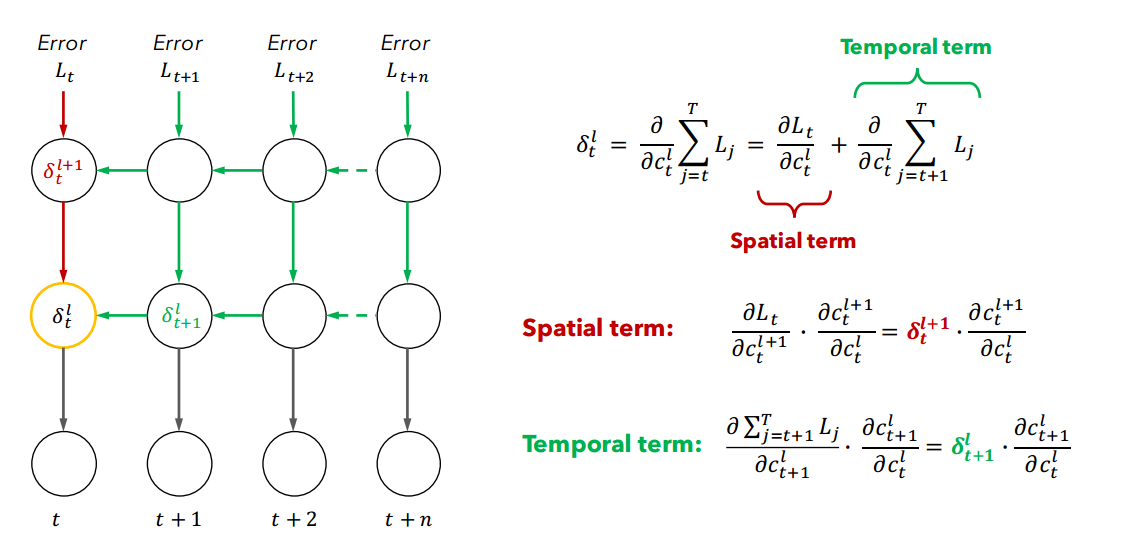
上图左边的网络结构表示的反向传播的过程。其中绿色的表示的是时间上的反向传播的过程,红色的是同一个时刻空间上的传播的过程(其实也就是普通前馈神经网络的误差过程),
上图右边的公式表示的反向传播的计算,n个输入的误差平方和的关于每个神经元的偏导(也就是$delta$),这个过程使用的是链式求导法则。而右边是关于$delta_{t}^{l}$的偏导。
第一个公式:将与$delta_{t}^{l}$同一个误差时刻(红色部分,也就是普通的前馈传播造成的误差)分离出来,其他时刻的误差(绿色部分)是时序上的,这个也是造成梯度消失或爆炸的原因。
第二个公式,$L_{t}$关于$c_{t}^{l}$的分解过程,这是BP网络的分解方式。
第三个公式,$sum L_{j}$关于$c_{t}^{l}$的分解过程,这和BP网络的分解方式类似。
2.2 BPTT算法存在的问题
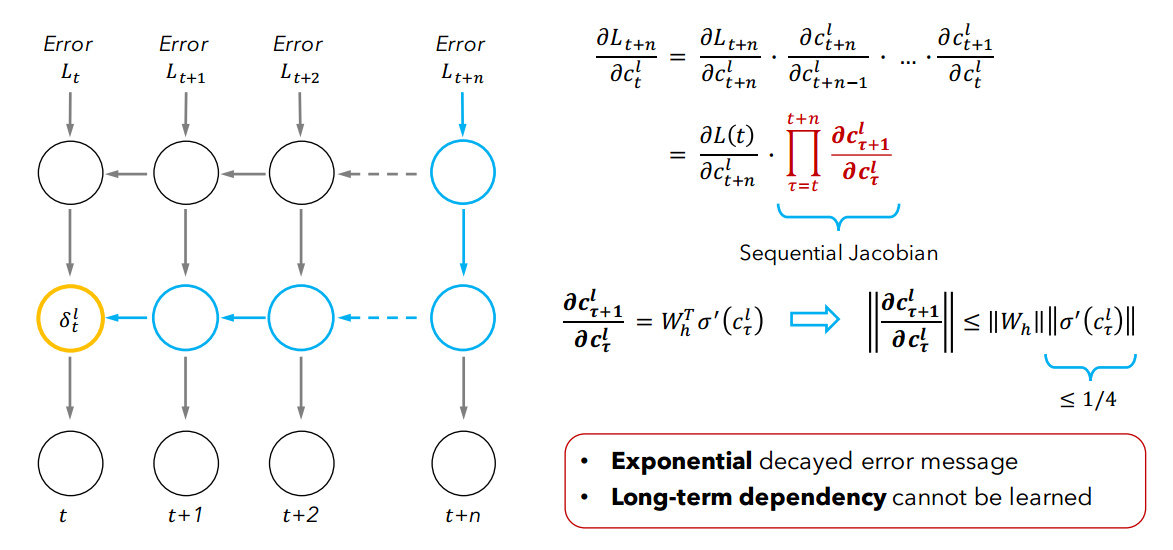
上图表示的是从$sum L_{j}$中取出最后一个$L_{t+n}$求关于$c_{t}^{l}$,存在n个$||W_{h}||||delta'(c_{ au}^{l})||$相乘,一般来说$||delta'(c_{ au}^{l})||$小于等于0.25,如果$W_{h}$小于4,那么就会出现梯度消;如果大于4,那么就会出现梯度爆炸。
2.3 解决方法:Constant Error Carrousel (CEC)
