插入排序
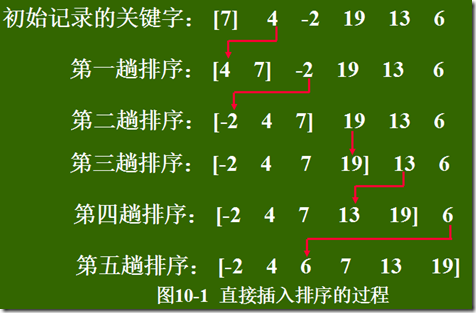
直接插入排序
/* 直接插入排序 */
void insertSort(int a[], int n)
{
int i,j;
for (i=2;i<=n;i++) // 依次将a[i]插入到前面已排序序列
{
if (a[i]<a[i-1]) // 若a[i]小于其前驱,才需将a[i]插入有序表
{
a[0]=a[i]; // 复制为哨兵
for (j=i-1;a[0]<a[j];--j) // 从后往前查找插入位置
{
a[j+1]=a[j]; // 向后挪位
}
a[j+1]=a[0]; // 复制到插入位置
}
}
}
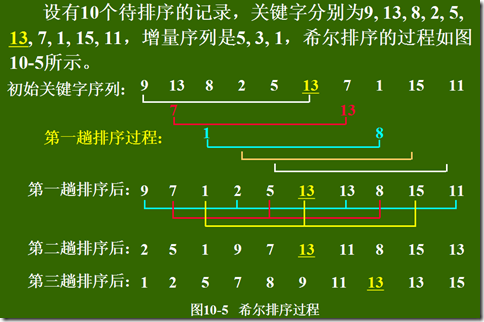
希尔排序
直接插入排序的时间复杂度为O(n2),但若待排序序列为正序时,其时间效率可提高至O(n)。希尔排序从以下两点分析出发对直接插入排序进行改进:
- 由于直接插入排序算法简单,则在n值很小时效率也比较高;
- 若待排序序列按关键字“基本有序”时,直接插入排序的效率可大大提高。
/* 希尔排序 */
void shellSort(int a[], int n)
{
// 对顺序表作希尔插入排序,本算法和直接插入排序相比,做了一下修改:
// 1> 前后记录位置的增量为dk,不是1
// 2> a[0]只是暂存单元,不是哨兵,当j<0时,插入位置已到
int dk,i,j;
for (dk=n/2;dk>=1;dk=dk/2) // 步长变化
{
for (i=dk+1;i<=n;i++)
{
if (a[i]<a[i-dk]) // 需将a[i]插入到有序增量子表
{
a[0]=a[i]; // 暂存在a[0]
for (j=i-dk;j>0&&a[0]<a[j];j-=dk)
{
a[j+dk]=a[j]; // 记录后移,查找插入的位置
}
a[j+dk]=a[0]; // 插入
}
}
}
}
交换排序
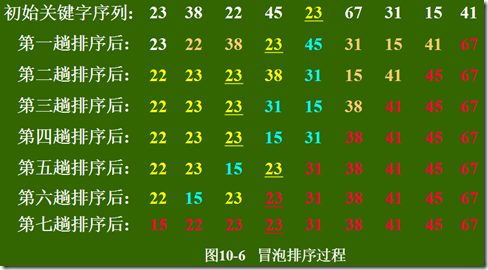
冒泡排序
/* 冒泡排序 */
void bubbleSort(int a[], int n)
{
int i,j;
for (i=0;i<n-1;i++) // 共有n-1趟排序
{
bool flag=false; // 表示本趟冒泡是否发生交换的标志
for (j=0;j<n-i-1;j++) // 一次冒泡过程
{
if (a[j]>a[j+1])
{
swap(a[j],a[j+1]);
flag=true;
}
}
if (flag==false)
{
break; // 本趟遍历后没有发生交换,说明表已经有序
}
}
}
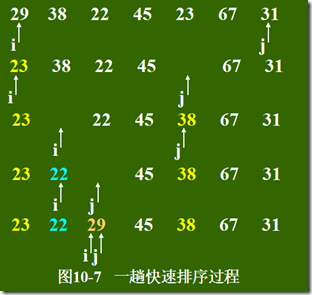
快速排序
参考之前文章:快速排序
// 一趟快速排序,划分
int partition(int a[],int low,int high)
{
int i=low,j=high;
int x = a[i];
while (i!=j)
{
while (a[j]>=x && i<j) j—;
if (i<j) { a[i]=a[j]; i++; }
while (a[i]<=x && i<j) i++;
if (i<j) { a[j]=a[i]; j—; }
}
a[i]=x;
return i;
}
/* 快速排序 */
void quickSort(int a[],int low,int high)
{
if (low<high)
{
int k = partition(a,low,high);
quickSort(a,low,k-1);
quickSort(a,k+1,high);
}
}
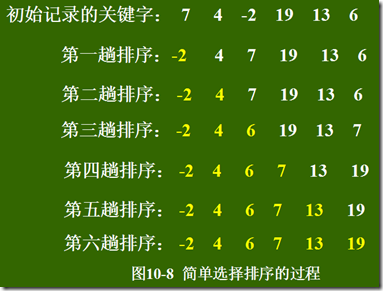
选择排序
简单选择排序
/* 简单选择排序 */
void selectSort(int a[], int n)
{
int i,j,min;
for (i=0;i<n-1;i++) // 共进行n-1趟
{
min=i; // 记录最小元素位置
for (j=i+1;j<n;j++) // 在a[i...n-1]中选择最小的元素
{
if (a[j]<a[min])
{
min=j; // 更新最小元素位置
}
if (min!=i)
{
swap(a[i],a[min]); // 最小元素与第i个位置交换
}
}
}
}
堆排序
参考之前的文章:堆排序
/* 向下调整,即筛选 */
void adjustDown(int a[], int start, int n)
{
// 根结点编号为1,对第start个元素进行调整
a[0]=a[start]; // a[0]暂存
for (int i=2*start;i<=n;i*=2) // 沿较大的子结点向下筛选
{
if (i<n&&a[i]<a[i+1])
{
i++; // 取较大的子结点的下标
}
if (a[0]>=a[i])
{
break; // 筛选结束
}
else
{
a[start]=a[i]; // 将a[i]调整到双亲结点上
start=i; // 修改start,以便继续向下筛选
}
}
a[start]=a[0]; // 被筛选结点的值放入最终位置
}
/* 堆排序 */
void heapSort(int a[], int n)
{
for (int i=n/2;i>0;i--) // 1> 初始建堆,从i=n/2 --> 1,反复向下调整
{
adjustDown(a,i,n);
}
for (int j=n;j>1;j--) // 2> n-1趟的交换和建堆过程
{
swap(a[j],a[1]); // 输出堆顶元素(和堆底元素交换)
adjustDown(a,1,j-1); // 把剩余的j-1个元素整理成堆
}
}
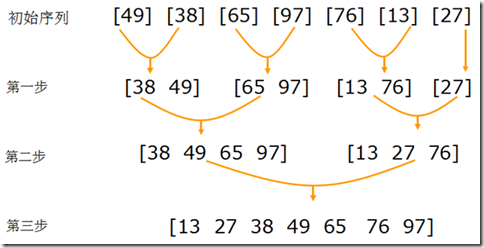
二路归并排序
参考之前的文章:二路归并排序
// 一趟归并排序算法
int b[N];
void merge(int a[],int left,int mid,int right)
{
// 表a的两段a[left..mid]和a[mid+1..right]各自有序,将它们合并成一个有序表
for (int m=left;m<=right;m++)
b[m] = a[m]; // 将a中所有元素复制到b中
for (int i=left,j=mid+1,k=i;i<=mid&&j<=right;k++)
{
if(b[i]<=b[j]) // 比较b的左右两段中的元素
a[k]=b[i++]; // 将较小值复制到a中
else
a[k]=b[j++];
}
while (i<=mid) a[k++]=b[i++]; // 若第一个表为检测完,复制
while (j<=right) a[k++]=b[j++]; // 若第二个表为检测完,复制
// 最后两个while循环只有一个会执行
}
/* 二路归并排序 */
void mergeSort(int a[],int left,int right)
{
if (left < right)
{
int mid = (left+right)/2; // 从中间划分两个子序列
mergeSort(a,left,mid); // 对左侧子序列进行递归排序
mergeSort(a,mid+1,right); // 对右侧子序列进行递归排序
merge(a,left,mid,right); // 归并
}
}